题目内容
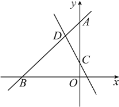
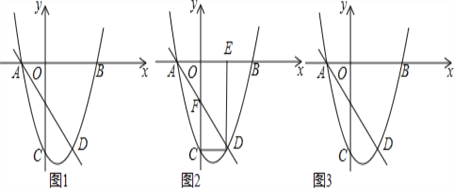
【题目】如图，在△ABC中，D为AB边上一点，E为CD中点，AC=
，∠ABC=30°，∠A=∠BED=45°，则BD的长为（ ）
A. 
B. 
+1﹣
C. ﹣ D. ﹣1
【答案】D
【解析】解：如图，过C作CF⊥AB于F，过点B作BG⊥CD于G．在Rt△BEG中，∠BED=45°，则GE=GB．在Rt△AFC中，∠A=45°，AC=
，则AF=CF=
=1．在Rt△BFC中，∠ABC=30°，CF=1，则BC=2CF=2，BF=
CF=，设DF=x，CE=DE=y，则BD=﹣x，∴△CDF∽△BDG，∴
=
=
，∴
=
=
，∴DG=
，BG=
．∵GE=GB，∴y+=，∴2y2+x（﹣x）=﹣x．在Rt△CDF中，∵CF2+DF2=CD2，∴1+x2=4y2，∴
+x（﹣x）=﹣x，整理得：x2﹣（2+2）x+2﹣1=0，解得：x=1+﹣
或1+﹣（舍弃），∴BD=﹣x=﹣1．故选D．
练习册系列答案
相关题目
