题目内容
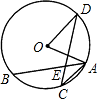如图，弦AB，CD相交于E点，若∠BAC=27°，∠BEC=64°，则∠AOD等于
- A.37°
- B.74°
- C.54°
- D.64°
B
分析：由∠BAC=27°，∠BEC=64°，根据三角形外角的性质，即可求得∠B的度数，又由圆周角定理，即可求得∠AOD的度数．
解答：∵∠BEC是△AEC的外角，
∴∠BEC=∠C+∠BAC，
∵∠BAC=27°，∠BEC=64°，
∴∠C=∠BEC-∠BAC=64°-27°=37°，
∴∠AOD=2∠C=2×37°=74°．
故选B．
点评：此题考查了圆周角定理与三角形外角的性质．此题难度不大，解题的关键是注意数形结合思想的应用，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半定理的应用．
分析：由∠BAC=27°，∠BEC=64°，根据三角形外角的性质，即可求得∠B的度数，又由圆周角定理，即可求得∠AOD的度数．
解答：∵∠BEC是△AEC的外角，
∴∠BEC=∠C+∠BAC，
∵∠BAC=27°，∠BEC=64°，
∴∠C=∠BEC-∠BAC=64°-27°=37°，
∴∠AOD=2∠C=2×37°=74°．
故选B．
点评：此题考查了圆周角定理与三角形外角的性质．此题难度不大，解题的关键是注意数形结合思想的应用，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半定理的应用．
练习册系列答案
相关题目
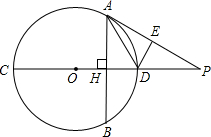如图，AB为⊙O内垂直于直径的弦，AB、CD相于点H，△AED与△AHD关于直线AD成轴对称．
的⊙O内有互相垂直的两条弦AB、CD相 交于P点。