题目内容
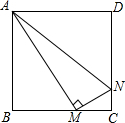 正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM=________cm时,四边形ABCN的面积最大,最大面积为________cm2.
正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM=________cm时,四边形ABCN的面积最大,最大面积为________cm2.


分析:设BM=xcm,则MC=1-xcm,当AM⊥MN时,利用互余关系可证△ABM∽△MCN,利用相似比求CN,根据梯形的面积公式表示四边形ABCN的面积,用二次函数的性质求面积的最大值.
解答:设BM=xcm,则MC=1-xcm,
∵∠AMN=90°,
∴∠AMB+∠NMC=90°,∠NMC+∠MNC=90°,
∴∠AMB=∠MNC,
又∵∠B=∠C
∴△ABM∽△MCN,则
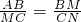 ,即
,即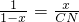 ,
,解得CN=
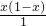 =x(1-x),
=x(1-x),∴S四边形ABCN=
 ×1×[1+x(1-x)]=-
×1×[1+x(1-x)]=- x2+
x2+ x+
x+ ,
,∵-
 <0,
<0,∴当x=-
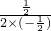 =
= cm时,S四边形ABCN最大,最大值是-
cm时,S四边形ABCN最大,最大值是- ×(
×( )2+
)2+ ×
× +
+ =
= cm2.
cm2.故答案是:
 ,
, .
.点评:本题考查了二次函数的性质的运用.关键是根据已知条件判断相似三角形,利用相似比求函数关系式.

练习册系列答案
相关题目
 附加题
附加题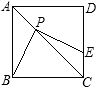 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3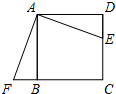 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=