题目内容
【题目】如图，反比例函数
的图象与直线
相交于
，
，点
是
轴上一动点．
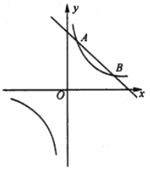
（1）①
_______；②当
时，的取值范围是_______；
（2）求反比例函数与直线的解析式；
（3）当
是等腰三角形时，求点的坐标．
【答案】（1）①2；②
或
；（2）反比例函数的解析式为
，直线的解析式为
；（3）
，
，
，
，
．
【解析】
（1）①首先根据A,B两点都在反比例函数图象上列出一个关系m的方程，解方程即可求出m的值；
②根据m的值进而求出A,B两点的坐标，数形结合即可得出不等式的解集；
（2）分别将A,B两点坐标代入一次函数与反比例函数的解析式中即可得出答案；
（3）根据等腰三角形的定义，分三种情况：
，
，
分别进行讨论即可．
解：（1）①∵点
，
都在反比例函数
图象上，
∴
解得
；
②∵，
∴
，
，
数形结合可知当
时，
的取值范围是或；
（2）∵点在反比例函数图象上，
∴
，
∴反比例函数的解析式为；
∵点
，
在直线
上，
∴
，解得
∴直线的解析式为；
（3）设点
，则
，
，
①当时，
，解得
，∴，
②当时，
，解得
，
，
∴，，
③当时，
，解得
，
，
∴，，
综上所述，，，，，．
练习册系列答案
相关题目
【题目】某商场经营某种品牌的计算器，购进时的单价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是600个，而销售单价每上涨1元，就会少售出10个．
（1）不妨设该种品牌计算器的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y个和销售该品牌计算器获得利润w元，并把结果填写在表格中：
销售单价（元） | x（x＞30） |
销售量y（个） |
|
销售计算器获得利润w（元） |
|
（2）在第（1）问的条件下，若计算器厂规定该品牌计算器销售单价不低于35元，且商场要完成不少于500个的销售任务，求：商场销售该品牌计算器获得最大利润是多少？
