题目内容
（1）如图1，在一次龙卷风中，一棵大树在离地面若干米处折断倒下，B为折断处最高点，树顶A落在离树根C的12米处，测得∠BAC=30°，求BC的长．（结果保留根号）
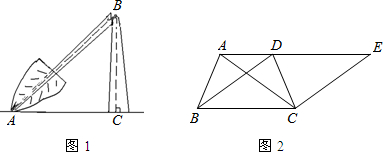
（2）如图2，等腰梯形ABCD中，AD∥BC，点E是AD延长线上一点，DE=BC．判断△ACE的形状并证明．
（2）如图2，等腰梯形ABCD中，AD∥BC，点E是AD延长线上一点，DE=BC．判断△ACE的形状并证明．
分析：（1）在三角形ABC中，根据tan∠BAC=
，再由∠BAC=30°，代入即可得出答案．
（2）先判断四边形BCED是平行四边形，再根据等腰梯形的性质可得出AC=BD，AC=EC，继而证出结论．
| BC |
| AC |
（2）先判断四边形BCED是平行四边形，再根据等腰梯形的性质可得出AC=BD，AC=EC，继而证出结论．
解答：解：（1）∵BC⊥AC，
∴∠BCA=90°
在直角△ABC中，
∵tan∠BAC=
，
∴BC=ACtan∠BAC=12×tan30°=12×
=4
．
（2）△ACE是等腰三角形
证明：∵AD∥BC，∴DE∥BC．
∵DE=BC，
∴四边形BCED是平行四边形，
∴BD=EC
又∵梯形ABCD是等腰梯形，
∴AC=BD，
∴AC=EC，
∴△ACE是等腰三角形．
∴∠BCA=90°
在直角△ABC中，
∵tan∠BAC=
| BC |
| AC |
∴BC=ACtan∠BAC=12×tan30°=12×
| ||
| 3 |
| 3 |
（2）△ACE是等腰三角形
证明：∵AD∥BC，∴DE∥BC．
∵DE=BC，
∴四边形BCED是平行四边形，
∴BD=EC
又∵梯形ABCD是等腰梯形，
∴AC=BD，
∴AC=EC，
∴△ACE是等腰三角形．
点评：此题考查了勾股定理的证明及等腰梯形的性质，解答本题的关键是掌握直角三角形中斜边的平方等于两直角边的平方和，及等腰梯形的两腰相等，难度一般．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
