题目内容
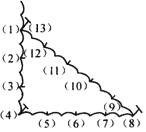
【题目】由一些正整数组成的数表如下（表中下一行中数的个数是上一行中数的个数的2倍）：
若规定坐标号（m,n）表示第m行从左向右第n个数，则（7，4）所表示的数是_____；（5，8）与（8，5）表示的两数之积是_______；数2012对应的坐标号是_________
【答案】134， 12144， （10，495）.
【解析】
根据下一行中数的个数是上一行中数的个数的2倍表示出前n行偶数的个数的表达式为2m-1，然后求出第6行的最后一个偶数，再计算之后的4个偶数即可求出（7，4）；分别求出第4行第7行最后的一个偶数，然后求出（5，8）与（8，5）表示的数，再相乘即可；求出数2012是第1006个偶数，根据表达式得1006=29-1+495，先求出第511个数是第9行的最后一个数，再求解即可．
解：设前m行偶数的个数为S，
则S=1+2+22+23+…+2m-1，
两边都乘以2得，2S=2+22+23+…+2m，
所以，S=2m-1，
当m=6时，S=26-1=64-1=63，
所以，（7，4）所表示的数是第63+4=67个偶数，为134；
当n=4时，24-1=15，
所以，（5，8）表示的数是第15+8=23个偶数，为46，
当n=7时，27-1=127，
所以，（8，5）表示的数是第127+5=132个偶数，为264，
46×264=12144；
∵数2012是第1006个偶数，
n=9时，29-1=511，1006-511=495
∴数2012是第10行的第495个数，可以表示为（10，495）．
故答案为：20，12144，（10，495）．
练习册系列答案
相关题目
