题目内容
如图，一零件的截面为直角梯形ABCD，AB∥DC，斜腰DA的长为12cm，∠D=135°，则该截面的另一腰BC的长是________cm．
6
分析：过D点作AB的垂线DE，DE的长和BC的长一样，根据条件可知△ADE是等腰直角三角形，从而可求出解．
解答：
解：作DE⊥AB于E点，
∵∠ADC=135°，
∴∠ADE=∠ADC-∠CDE=135°-90°=45°，
∴AE=DE．
∵DA=12，
∴AE2+DE2=122，
∴DE=6，
∴BC=DE=6．
故答案为：6．
点评：本题考查直角梯形的性质，直角梯形有两个角是直角，作辅助线可求出解．
分析：过D点作AB的垂线DE，DE的长和BC的长一样，根据条件可知△ADE是等腰直角三角形，从而可求出解．
解答：
解：作DE⊥AB于E点，∵∠ADC=135°，
∴∠ADE=∠ADC-∠CDE=135°-90°=45°，
∴AE=DE．
∵DA=12，
∴AE2+DE2=122，
∴DE=6
，∴BC=DE=6
．故答案为：6
．点评：本题考查直角梯形的性质，直角梯形有两个角是直角，作辅助线可求出解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，一零件的截面为直角梯形ABCD，AB∥DC，斜腰DA的长为12cm，∠D=135°，则该截面的另一腰BC的长是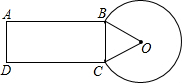
（1997•上海）如图，一种零件的横截面积是由矩形、三角形和扇形组成，矩形的长AB=2.45cm，扇形所在的圆的半径OB=1cm，扇形的弧所对的圆心角为300°，求这种零件的横截面的面积．（精确到0.01cm2，π≈3.142，
