Question

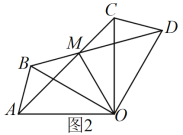
【题目】如图，△ABC和△CDE都是等边三角形，且∠EBD=72°，则∠AEB的度数是______．

Answer 1

【答案】132°

【解析】

由已知条件推导出△ACE≌△BCD，从而∠DBC=∠CAE，再通过角之间的转化，利用三角形内角和定理能求出∠AEB的度数．

解：∵△ABC和△CDE都是等边三角形，且∠EBD=72°，

∴AC=BC，CE=CD，∠ACB=∠ECD=60°，

又∵∠ACB=∠ACE+∠BCE，∠ECD=∠BCE+∠BCD，

∴∠BCD=∠ACE，

∴△ACE≌△BCD，

∴∠DBC=∠CAE，

∴72°∠EBC=60°∠BAE，

∴72°（60°∠ABE）=60°∠BAE，

∴∠ABE+∠BAE=48°，

∴∠AEB=180°（∠ABE+∠BAE）=180°48°=132°．

故答案为：132°．