题目内容
 如图,⊙O中有直径AB、EF和弦BC,且BC和EF交于点D.点D是弦BC的中点,CD=4.DF=8.
如图,⊙O中有直径AB、EF和弦BC,且BC和EF交于点D.点D是弦BC的中点,CD=4.DF=8.
(1)求⊙O的半径R及线段AD的长;
(2)求sin∠DAO的值.
 解:(1)∵D是BC的中点,EF是直径,
解:(1)∵D是BC的中点,EF是直径,∴CB⊥EF且BD=CD=4.…
∵DF=8,
∴OD=8-R,
∵OB2-OD2=DB2,
∴R2-(8-R)2=42,
∴R=5.…
连续AC,过D作DH⊥AB交AB于H.
∵AB是直径,
∴∠ACB=90°.
∵CB=2CD=8,AB=10,
∴AC=6.
∴∠ACD=90°,AC=6,CD=4,
∴AD=2
 .…
.…(2)∵Rt△DHB中,DH=DB•sin∠DBH=4×
 =
= ,…
,…∴sin∠DAO=
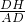 =
= .…
.…分析:(1)由点D是弦BC的中点,EF是直径,根据垂径定理的推论,即可得CB⊥EF且BD=CD=4,然后利用勾股定理,即可求得⊙O的半径R;再连续AC,过D作DH⊥AB交AB于H,由AB是直径,即可得∠ACB=90°,继而可求得线段AD的长;
(2)在Rt△DHB中,由DH=DB•sin∠DBH,可求得DH的长,又由sin∠DAO=
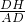 ,求得答案.
,求得答案.点评:此题考查了圆周角定理、垂径定理、勾股定理以及三角函数等知识.此题难度适中,解题的关键是掌握数形结合思想与方程思想的应用,注意辅助线的作法.

练习册系列答案
相关题目
 如图,⊙O中有直径AB、EF和弦BC,且BC⊥EF于点D,CB=DF=8.
如图,⊙O中有直径AB、EF和弦BC,且BC⊥EF于点D,CB=DF=8. (2012•房山区二模)如图,⊙O中有直径AB、EF和弦BC,且BC和EF交于点D.点D是弦BC的中点,CD=4.DF=8.
(2012•房山区二模)如图,⊙O中有直径AB、EF和弦BC,且BC和EF交于点D.点D是弦BC的中点,CD=4.DF=8.
