题目内容
如图,直线y=2x+2与x轴、y轴分别相交于A、B两点,将△AOB绕点O顺时针旋转90°得到△A1OB1.
(1)在图中画出△A1OB1;
(2)求经过A,A1,B1三点的抛物线的解析式.

考点:
待定系数法求二次函数解析式;作图-旋转变换.
专题:
作图题;数形结合.
分析:
本题是在直角坐标系中,对直线进行旋转的问题,实质上就是把A,B两点绕O点顺时针旋转90°可以根据坐标轴的垂直关系画图.再根据已知三点A,A1,B1的坐标,确定抛物线解析式.
解答:
解:(1)如右图.(2)设该抛物线的解析式为:y=ax2+bx+c.
由题意知A、A1、B1三点的坐标分别是(﹣1,0)、(0,1)、(2,0).
∴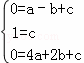 ,
,
解这个方程组得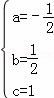 .
.
∴抛物线的解析式是:y=﹣![]() x2+
x2+![]() x+1.
x+1.
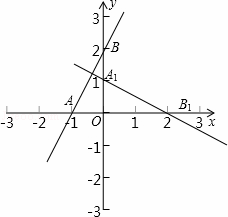
点评:
本题要充分运用形数结合的方法,在坐标系中对图形旋转,根据一次函数解析式求点的坐标,又根据点的坐标求二次函数解析式.

练习册系列答案
相关题目
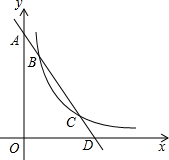 如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线
如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线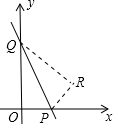 如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是
如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是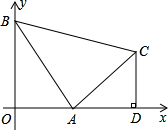 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F. 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.