Question

（2013•滨湖区一模）如图，AB是半圆O的直径，AB=10，过点A的直线交半圆于点C，且AC=6，连结BC，点D为BC的中点．已知点E在直线AC上，△CDE与△ACB相似，则线段AE的长为

3或

2

3

或9或

34

3

．

Answer 1

分析：根据E点在直线AC上，得出对应点不同求出的EC长度不同，分别得出即可．

解答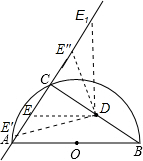：解：∵AB是半圆O的直径，
∴∠ACB=90°，
∵AB=10，AC=6，
∴BC=

102-62

=8，
∵点D为BC的中点，
∴CD=4，
当DE∥AB时，
△CED∽△CAB，
∴

CE

AC

=

CD

BC

，
∴

EC

6

=

4

8

，
解得：EC=3，
∴AE=6-EC=3，
当

CD

AC

=

CE′

CB

，且∠ACB=∠DCE′时，△CE′D∽△CBA，
则

4

6

=

CE′

8

，
解得：CE′=

16

3

，
∴AE′=6-

16

3

=

2

3

；
当

CD

AC

=

CE1

BC

，且∠ACB=∠DCE₁时，△CE₁D∽△CBA，
则

4

6

=

CE1

8

，
解得：CE₁=

16

3

，
∴AE₁=6+

16

3

=

34

3

；
当

CD

BC

=

E″C

AC

，且∠ACB=∠DCE″时，△CE″D∽△CBA，
则

4

8

=

E″C

6

，
解得：CE″=3，
∴AE″=6+3=9；
综上所述：点E在直线AC上，△CDE与△ACB相似，则线段AE的长为3或

2

3

或9或

34

3

．
故答案为：3或

2

3

或9或

34

3

．

点评：此题主要考查了相似三角形的判定与性质，注意在直线AC上有一点E，进行分类讨论得出是解题关键．