题目内容
若圆的半径为R,则它的内接正方形的边长为
- A.
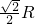
- B.R
- C.
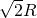
- D.2R
C
分析:先由题意画出图形,根据正方形的特点判断出△OBC的形状,再根据勾股定理求出BC的长即可.
解答: 解:如图所示,连接OB、OC;
解:如图所示,连接OB、OC;
∵四边形ABCD是正方形,
∴∠BOC= =90°,
=90°,
∴BC= =
= =
= R.
R.
故选C.
点评:此题比较简单,解答此题的关键是画出图形,根据数形结合解答.
分析:先由题意画出图形,根据正方形的特点判断出△OBC的形状,再根据勾股定理求出BC的长即可.
解答:
 解:如图所示,连接OB、OC;
解:如图所示,连接OB、OC;∵四边形ABCD是正方形,
∴∠BOC=
 =90°,
=90°,∴BC=
 =
= =
= R.
R.故选C.
点评:此题比较简单,解答此题的关键是画出图形,根据数形结合解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若圆的半径为R,则它的内接正方形的边长为( )
A、
| ||||
| B、R | ||||
C、
| ||||
| D、2R |

