Question

【题目】已知：如图，在平面直角坐标系xOy中，A（4，0），C（0，6），点B在第一象限内，点P从原点O出发，以每秒2个单位长度的速度沿着长方形OABC移动一周（即：沿着O→A→B→C→O的路线移动）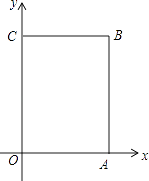

（1）写出B点的坐标（）；
（2）当点P移动了4秒时，在图中平面直角坐标系中描出此时P点的位置，并求出点P的坐标；
（3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间t．

Answer 1

【答案】
（1）4,6
（2）解：由每秒2个单位长度的速度沿着长方形OABC移动一周（即：沿着O→A→B→C→O的路线移动），

点P移动了4秒，得P点移动了8个单位，即OA+AP=8，

P点在AB上且距A点4个单位，

P（4，4）

（3）解：第一次距x轴5个单位时AP=5，即OA+AP=9=2t，

解得t= ，

第二次距x轴5个单位时，OP=5，即 OA+AB+BC+CP=4+6+4+6﹣5=2t，解得t= ，

综上所述：t= 秒，或t= 秒时，点P到x轴的距离为5个单位长度．

【解析】解：（1）由矩形的性质，得

CB=OA=4，AB=OC=6，

B（4，6）；

故答案为：4，6；

（1）根据矩形的对边相等，可得CB，AB的长，根据点的坐标表示方法，可得答案；（2）根据速度乘时间等于路程，可得OA+AP的长度，根据点的坐标表示方法，可得答案；（3）分类讨论：①OA+AP=9=2t，②OA+AB+BC+CP=4+6+4+6﹣5=2t，根据解方程，可得答案．