题目内容
已知在△ABC中,∠A、∠B是锐角,且sinA= ,tanB=2,AB=29cm,则△ABC的面积等于________cm2.
,tanB=2,AB=29cm,则△ABC的面积等于________cm2.
145
分析:过点C作AB的垂线,得到两个直角三角形,根据题意求出两直角三角形中AD,DB和CD的长,用三角形的面积公式求出三角形的面积.
解答: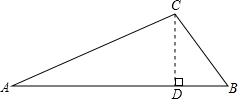 解:如图:
解:如图:
过点C作AB的垂线,垂足为D.
∵sinA= =
= ,
,
设CD=5x,AC=13x(x>0).
∵tanB= =2,
=2,
可设CD=2y,BD=y(y>0),
∴BD=y=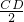 =
= x.
x.
∴AD=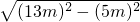 =12x.
=12x.
从而得AB=AD+BD=12x+ x=
x=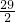 x.
x.
由29=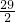 x,得x=2.
x,得x=2.
则CD=5x=10.
故S△ABC= AB•CD=
AB•CD= ×29×10=145(cm2).
×29×10=145(cm2).
故答案是:145.
点评:本题考查的是解直角三角形,过点C作AB的垂线得到两个直角三角形,由∠A的正弦和∠B的正切值,得到直角三角形中边的关系,求出AB和CD的长,用三角形的面积公式求出三角形的面积.
分析:过点C作AB的垂线,得到两个直角三角形,根据题意求出两直角三角形中AD,DB和CD的长,用三角形的面积公式求出三角形的面积.
解答:
 解:如图:
解:如图:过点C作AB的垂线,垂足为D.
∵sinA=
 =
= ,
,设CD=5x,AC=13x(x>0).
∵tanB=
 =2,
=2,可设CD=2y,BD=y(y>0),
∴BD=y=
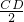 =
= x.
x.∴AD=
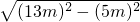 =12x.
=12x.从而得AB=AD+BD=12x+
 x=
x=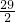 x.
x.由29=
 x,得x=2.
x,得x=2.则CD=5x=10.
故S△ABC=
 AB•CD=
AB•CD= ×29×10=145(cm2).
×29×10=145(cm2).故答案是:145.
点评:本题考查的是解直角三角形,过点C作AB的垂线得到两个直角三角形,由∠A的正弦和∠B的正切值,得到直角三角形中边的关系,求出AB和CD的长,用三角形的面积公式求出三角形的面积.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.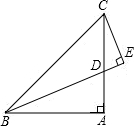 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.