题目内容
经过长方形对称中心的任意一条直线把长方形分成面积分别为S1和S2的两部分，那么S1和S2的大小关系为________．
S1=S2
分析：根据矩形对角线相等且平分的性质，易证△OEC≌△OFA，△DEO≌△BFO，△AOD≌△BOC，即可证明S1=S2，即可解题．
解答：
解：矩形ABCD中，AD=BC，
AO=BO=CO=DO，
在△AOD和△BOC中
∴△AOD≌△BOC（SAS），
∵∠ECO=∠FAO，OA=OC，∠EOC=∠FOA，
在△OEC和△OFA中
∴△OEC≌△OFA（ASA），
同理可证，△DEO≌△BFO，
∴S1=S2．
故答案为：S1=S2．
点评：本题考查了矩形对角线相等且互相平分的性质，全等三角形的证明，全等三角形面积相等的性质，本题中求证△OEC≌△OFA是解题的关键．
分析：根据矩形对角线相等且平分的性质，易证△OEC≌△OFA，△DEO≌△BFO，△AOD≌△BOC，即可证明S1=S2，即可解题．
解答：
解：矩形ABCD中，AD=BC，AO=BO=CO=DO，
在△AOD和△BOC中
∴△AOD≌△BOC（SAS），
∵∠ECO=∠FAO，OA=OC，∠EOC=∠FOA，
在△OEC和△OFA中
∴△OEC≌△OFA（ASA），
同理可证，△DEO≌△BFO，
∴S1=S2．
故答案为：S1=S2．
点评：本题考查了矩形对角线相等且互相平分的性质，全等三角形的证明，全等三角形面积相等的性质，本题中求证△OEC≌△OFA是解题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
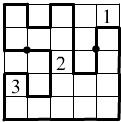
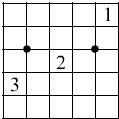在图5×5和方格中，沿着已有的线画一个简单连续的闭合圈作篱笆，篱笆不能“自身相交”．小方格中的数表示这小方格上属于篱笆的边数（如
），篱笆经过两个黑点，而且对于以“黑点”为中心的长方形，它边上的篱笆也以这个黑点为对称中心．
