题目内容
 如图,已知∠APC=30°,
如图,已知∠APC=30°, |
| BD |
 |
| AC |
分析:连接AC,由
=30°可求出∠1=∠2=15°,再由三角形外角的性质可求出∠ADC的度数,进而得出
的度数,再根据∠AEC是△AEC的外角即可得出∠AEC的度数.
 |
| BD |
 |
| AC |
解答: 解:连接AC,
解:连接AC,
∵
=30°,
∴∠1=∠2=
=15°,
∵∠APC=30°,∠ADC是△APD的外角,
∴∠ADC=∠1+∠APC=15°+30°=45°,
∴
=2∠ADC=90°;
∵∠AEC是△CDE的外角,
∴∠AEC=∠ADC+∠2=45°+15°=60°.
故答案为:90°,60°.
 解:连接AC,
解:连接AC,∵
 |
| BD |
∴∠1=∠2=
| 1 |
| 2 |
 |
| BD |
∵∠APC=30°,∠ADC是△APD的外角,
∴∠ADC=∠1+∠APC=15°+30°=45°,
∴
 |
| AC |
∵∠AEC是△CDE的外角,
∴∠AEC=∠ADC+∠2=45°+15°=60°.
故答案为:90°,60°.
点评:本题考查的是圆心角、弧、弦的关系及三角形外角的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
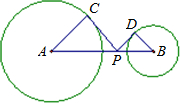 如图,已知⊙A半径为2,⊙B半径为1,AB=4,P为线段AB上的动点,且PC切⊙A于点C,PD切⊙B于点D.
如图,已知⊙A半径为2,⊙B半径为1,AB=4,P为线段AB上的动点,且PC切⊙A于点C,PD切⊙B于点D.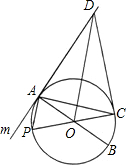 如图,已知⊙O的直径AB=2,直线m与⊙O相切于点A,P为⊙O上一动点(与点A、点B不重合),PO的延长线与⊙O相交于点C,过点C的切线与直线m相交于点D.
如图,已知⊙O的直径AB=2,直线m与⊙O相切于点A,P为⊙O上一动点(与点A、点B不重合),PO的延长线与⊙O相交于点C,过点C的切线与直线m相交于点D. 如图,已知∠APC=30°,
如图,已知∠APC=30°, 的度数为30°,求
的度数为30°,求 和∠AEC的度数.
和∠AEC的度数. 的度数为30°,求
的度数为30°,求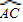 和∠AEC的度数.
和∠AEC的度数.