题目内容
设x、y、z是三个实数,且有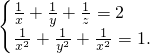 ,则
,则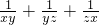 的值是
的值是
- A.1
- B.

- C.

- D.

C
分析:首先把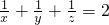 通分变为
通分变为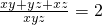 ,接着得到xy+yz+zx=2xyz,然后两边同时平方得到x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,然后把
,接着得到xy+yz+zx=2xyz,然后两边同时平方得到x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,然后把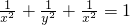 通分变为
通分变为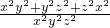 =1,然后变为x2y2+y2z2+z2x2=x2y2z2,接着把它代入①中即可解决问题.
=1,然后变为x2y2+y2z2+z2x2=x2y2z2,接着把它代入①中即可解决问题.
解答:∵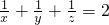 ,
,
∴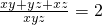 ,
,
∴xy+yz+zx=2xyz,
两边平方得
x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,
又∵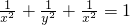 ,
,
∴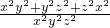 =1,
=1,
∴x2y2+y2z2+z2x2=x2y2z2②,
把②代入①得
x2y2z2+2xyz(x+y+z)=4x2y2z2,
∴2xyz(x+y+z)=3x2y2z2,
∴xyz(x+y+z)=3x2y2z2÷2,
两边同时除以x2y2z2得
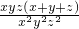 =
= ,
,
∴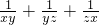 =
= .
.
故选C.
点评:此题主要考查了利用完全平方公式进行恒等式变形然后求代数式的值,是一个竞赛题,比较难,要求学生对于完全平方公式和代数变形比较熟练才能很好的解决问题.
分析:首先把
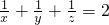 通分变为
通分变为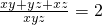 ,接着得到xy+yz+zx=2xyz,然后两边同时平方得到x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,然后把
,接着得到xy+yz+zx=2xyz,然后两边同时平方得到x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,然后把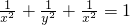 通分变为
通分变为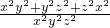 =1,然后变为x2y2+y2z2+z2x2=x2y2z2,接着把它代入①中即可解决问题.
=1,然后变为x2y2+y2z2+z2x2=x2y2z2,接着把它代入①中即可解决问题.解答:∵
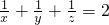 ,
,∴
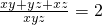 ,
,∴xy+yz+zx=2xyz,
两边平方得
x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,
又∵
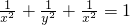 ,
,∴
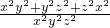 =1,
=1,∴x2y2+y2z2+z2x2=x2y2z2②,
把②代入①得
x2y2z2+2xyz(x+y+z)=4x2y2z2,
∴2xyz(x+y+z)=3x2y2z2,
∴xyz(x+y+z)=3x2y2z2÷2,
两边同时除以x2y2z2得
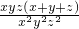 =
= ,
,∴
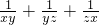 =
= .
.故选C.
点评:此题主要考查了利用完全平方公式进行恒等式变形然后求代数式的值,是一个竞赛题,比较难,要求学生对于完全平方公式和代数变形比较熟练才能很好的解决问题.

练习册系列答案
相关题目
1.红用下面的方法对![]() 进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
| 方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 关于x的方程
( 且 |
|
|
|
2.设![]() 是一元二次方程
是一元二次方程![]()
![]() 的两个实根,根据观察表格中的规律,写出二次三项式
的两个实根,根据观察表格中的规律,写出二次三项式![]()
![]() 的因式分解与
的因式分解与![]() 之间的关系式。
之间的关系式。
1.红用下面的方法对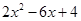 进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
|
方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
关于x的方程
( 且 |
|
|
|
2.设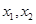 是一元二次方程
是一元二次方程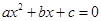
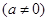 的两个实根,根据观察表格中的规律,写出二次三项式
的两个实根,根据观察表格中的规律,写出二次三项式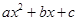
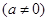 的因式分解与
的因式分解与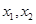 之间的关系式。
之间的关系式。

 +k)k,k为实数.
+k)k,k为实数. 是否为一定值?若是,请求出该定值;若不是,请说明理由;
是否为一定值?若是,请求出该定值;若不是,请说明理由;












 、
、 、
、 为常数,
为常数, )
)
