题目内容
如图,将矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上点P处,已知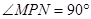 ,PM=3,PN=4,,那么矩形纸片ABCD的面积为 .
,PM=3,PN=4,,那么矩形纸片ABCD的面积为 .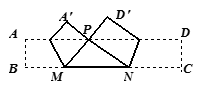
 ,PM=3,PN=4,,那么矩形纸片ABCD的面积为 .
,PM=3,PN=4,,那么矩形纸片ABCD的面积为 .

试题分析:将矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上点P处,BM=PM,CN=PN;已知
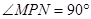 ,PM=3,PN=4,在
,PM=3,PN=4,在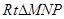 中由勾股定理得
中由勾股定理得 ,根据直角三角形的面积公式,在
,根据直角三角形的面积公式,在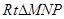 中
中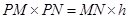 ,解得h=
,解得h=  ,由题意得
,由题意得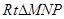 边MN上高与矩形的宽相等,所以AB=
边MN上高与矩形的宽相等,所以AB= ;因为BC=BM+MN+NC=3+5+4=12,所以矩形纸片ABCD的面积=
;因为BC=BM+MN+NC=3+5+4=12,所以矩形纸片ABCD的面积=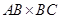 =
=
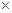 12=
12=
点评:本题考查折叠, 矩形,勾股定理,要求考生掌握折叠的特征,矩形的性质,以及勾股定理的内容

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目





 中至多有一个直角或钝角”的反设是 .
中至多有一个直角或钝角”的反设是 .
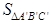 = ;
= ;