题目内容
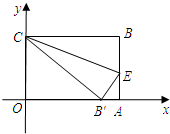 如图,在直角坐标系中放入一个边长OC为12的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=
如图,在直角坐标系中放入一个边长OC为12的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C= .
.
(1)求B′点的坐标;
(2)求折痕CE的长.
解:(1)∵四边形OABC是矩形,
∴∠AOC=90°,
∵tan∠OB′C= ,OC=12,
,OC=12,
∴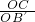 =
= ,
,
解得:OB′=16,
∴B′点的坐标为:(16,0);
(2)由折叠的性质可得:∠AB′E=∠B=90°,BE=B′E,
∴∠OB′C+∠AB′E=90°,∠AB′E+∠AEB′=90°,
∴∠AEB′=∠OB′E,
∴tan∠AEB′= ,
,
∴cos∠AEB′= ,
,
设BE=x,则AE=AB-BE=12-x,
∴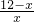 =
= ,
,
解得:x= ,
,
∴BE= ,AE=
,AE= ,
,
∴AB′=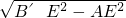 =4,
=4,
∴BC=OA=OB′+AB′=20,
∴CE=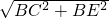 =
=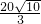 .
.
分析:(1)由四边形OABC是矩形,边长OC为12,tan∠OB′C= ,利用三角函数的知识即可求得OB′的长,继而求得答案;
,利用三角函数的知识即可求得OB′的长,继而求得答案;
(2)易证得∠AEB′=∠OB′C,然后利用三角函数的性质,即可求得BE、AE的长,然后由勾股定理求得答案.
点评:此题考查了折叠的性质、矩形的性质、三角函数的定义以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想与方程思想的应用.
∴∠AOC=90°,
∵tan∠OB′C=
 ,OC=12,
,OC=12,∴
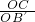 =
= ,
,解得:OB′=16,
∴B′点的坐标为:(16,0);
(2)由折叠的性质可得:∠AB′E=∠B=90°,BE=B′E,
∴∠OB′C+∠AB′E=90°,∠AB′E+∠AEB′=90°,
∴∠AEB′=∠OB′E,
∴tan∠AEB′=
 ,
,∴cos∠AEB′=
 ,
,设BE=x,则AE=AB-BE=12-x,
∴
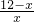 =
= ,
,解得:x=
 ,
,∴BE=
 ,AE=
,AE= ,
,∴AB′=
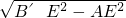 =4,
=4,∴BC=OA=OB′+AB′=20,
∴CE=
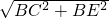 =
=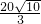 .
.分析:(1)由四边形OABC是矩形,边长OC为12,tan∠OB′C=
 ,利用三角函数的知识即可求得OB′的长,继而求得答案;
,利用三角函数的知识即可求得OB′的长,继而求得答案;(2)易证得∠AEB′=∠OB′C,然后利用三角函数的性质,即可求得BE、AE的长,然后由勾股定理求得答案.
点评:此题考查了折叠的性质、矩形的性质、三角函数的定义以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: