题目内容
抛物线y=-x2+4x-2的顶点与原点之间的距离为________．
2
分析：先把抛物线化为顶点式，再求出其顶点坐标，根据两点间的距离公式结论即可．
解答：∵抛物线y=-x2+4x-2可化为y=-（x-2）2+2，
∴其顶点坐标为（2，2），
∴顶点与原点之间的距离=
=2．
故答案为：2．
点评：本题考查的是二次函数的性质，熟知二次函数的顶点式是解答此题的关键．
分析：先把抛物线化为顶点式，再求出其顶点坐标，根据两点间的距离公式结论即可．
解答：∵抛物线y=-x2+4x-2可化为y=-（x-2）2+2，
∴其顶点坐标为（2，2），
∴顶点与原点之间的距离=
=2．故答案为：2
．点评：本题考查的是二次函数的性质，熟知二次函数的顶点式是解答此题的关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
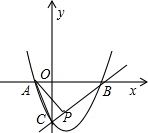A是抛物线与x轴的另一个交点．
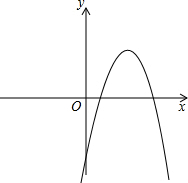已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是