题目内容
如图所示,在⊙O中,AB是直径,CD是弦,AB⊥CD,AB=12cm.(1)F是
 上一点(不与C、D重合),求证:∠CFD=∠COB;
上一点(不与C、D重合),求证:∠CFD=∠COB;(2)若∠CFD=60°,求CD的长.

【答案】分析:(1)已知直径AB⊥CD,由垂径定理知B是弧CD的中,若连接OD,可证得∠COB是∠COD的一半;由圆周角定理知:∠CFD= ∠COD,由此得证;
∠COD,由此得证;
(2)若∠CFD=60°,则∠COB=60°,通过解直角三角形即可求得CD的长.
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵AB是直径,AB⊥CD,∴ =
= ,
,
∴∠COB=∠DOB= ,
,
∴∠CFD=∠COB.
(2)解:Rt△COE中,OC=6cm,∠COE=∠CFD=60°;
∴CE=OC•sin60°=3 cm;
cm;
∴CD=2CE= cm.
cm.
点评:此题主要考查圆周角定理、垂径定理及解直角三角形的应用.
 ∠COD,由此得证;
∠COD,由此得证;(2)若∠CFD=60°,则∠COB=60°,通过解直角三角形即可求得CD的长.
解答:
 (1)证明:连接OD,
(1)证明:连接OD,∵AB是直径,AB⊥CD,∴
 =
= ,
,∴∠COB=∠DOB=
 ,
,∴∠CFD=∠COB.
(2)解:Rt△COE中,OC=6cm,∠COE=∠CFD=60°;
∴CE=OC•sin60°=3
 cm;
cm;∴CD=2CE=
 cm.
cm.点评:此题主要考查圆周角定理、垂径定理及解直角三角形的应用.

练习册系列答案
相关题目
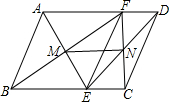 如图所示,在?ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF交于点M,连接CF,DE交于点N,求证:MN∥AD且MN=
如图所示,在?ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF交于点M,连接CF,DE交于点N,求证:MN∥AD且MN= 如图所示,在△ABC中,∠C=90°,D是AC边上一点,且AD=DB=5,CD=3,求tan∠CBD和sinA.
如图所示,在△ABC中,∠C=90°,D是AC边上一点,且AD=DB=5,CD=3,求tan∠CBD和sinA.

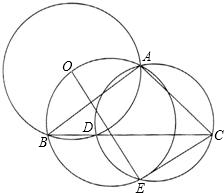 如图所示,在△ABC中,已知D是BC边上的点,O为△ABD的外接圆圆心,△ACD的外接圆与△AOB的外接圆相交于A,E两点.求证:OE⊥EC.
如图所示,在△ABC中,已知D是BC边上的点,O为△ABD的外接圆圆心,△ACD的外接圆与△AOB的外接圆相交于A,E两点.求证:OE⊥EC.