题目内容
 如图所示,将宽为4厘米的纸条折叠,折痕为AB,如果∠ACB=30°,折叠后重叠部分的面积为_____平方厘米.
如图所示,将宽为4厘米的纸条折叠,折痕为AB,如果∠ACB=30°,折叠后重叠部分的面积为_____平方厘米.
- A.16
- B.14
- C.12
- D.4
A
分析:根据翻折不变性,得到∠α=∠CAB,从而求出∠ABC=∠BAC,再得出△ACB为等腰三角形,求出AD和CB的长,进而求出△ABC的面积.
解答: 解:延长GA到F,根据翻折不变性,∠α=∠CAB,
解:延长GA到F,根据翻折不变性,∠α=∠CAB,
∵AG∥BC,
∴∠GAC=∠ACB=30°,
∴∠α=∠CAB=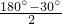 =75°,
=75°,
∴∠ABC=180°-30°-75°=75°,
∴AC=BC.
作AD⊥BC,垂足为D,
∵纸条的宽=4cm,
∴AD=4cm,
在Rt△ACD中,∠ACD=30°,
∴AC=2AD=2×4=8cm,
∴AC=BC=8cm,
∴△ABC的面积为 ×4×8=16cm.
×4×8=16cm.
故选A.
点评:此题考查了翻折不变性和平行线的性质和等腰三角形的性质及含30°的角的性质,综合性较强.
分析:根据翻折不变性,得到∠α=∠CAB,从而求出∠ABC=∠BAC,再得出△ACB为等腰三角形,求出AD和CB的长,进而求出△ABC的面积.
解答:
 解:延长GA到F,根据翻折不变性,∠α=∠CAB,
解:延长GA到F,根据翻折不变性,∠α=∠CAB,∵AG∥BC,
∴∠GAC=∠ACB=30°,
∴∠α=∠CAB=
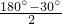 =75°,
=75°,∴∠ABC=180°-30°-75°=75°,
∴AC=BC.
作AD⊥BC,垂足为D,
∵纸条的宽=4cm,
∴AD=4cm,
在Rt△ACD中,∠ACD=30°,
∴AC=2AD=2×4=8cm,
∴AC=BC=8cm,
∴△ABC的面积为
 ×4×8=16cm.
×4×8=16cm.故选A.
点评:此题考查了翻折不变性和平行线的性质和等腰三角形的性质及含30°的角的性质,综合性较强.

练习册系列答案
相关题目
 如图所示,将宽为4厘米的纸条折叠,折痕为AB,如果∠ACB=30°,折叠后重叠部分的面积为( )平方厘米.
如图所示,将宽为4厘米的纸条折叠,折痕为AB,如果∠ACB=30°,折叠后重叠部分的面积为( )平方厘米.| A、16 | B、14 | C、12 | D、4 |

 34、“元旦”节快到了,张华想为自己的爸爸、妈妈送一件礼物,对父母一年来的辛苦表示一点心意.他亲自制作了一个小礼物,并且想用一个无盖的长方体盒子将其装起来.如图所示,正好有一张长为32厘米,宽为24厘米的包装纸,张华想在四个角上截去四个相同的小正方形,然后做成底面周长为64厘米的没有盖的长方体盒子,用来装礼物,请你帮小华设计一下,截去的小正方形的边长应是多少?
34、“元旦”节快到了,张华想为自己的爸爸、妈妈送一件礼物,对父母一年来的辛苦表示一点心意.他亲自制作了一个小礼物,并且想用一个无盖的长方体盒子将其装起来.如图所示,正好有一张长为32厘米,宽为24厘米的包装纸,张华想在四个角上截去四个相同的小正方形,然后做成底面周长为64厘米的没有盖的长方体盒子,用来装礼物,请你帮小华设计一下,截去的小正方形的边长应是多少?