��Ŀ����
����Ŀ����ͼ���������ϵ�![]() ��ʾ��
��ʾ��![]() ����
����![]() ��ʾ��
��ʾ��![]() ����
����![]() ��ʾ��
��ʾ��![]() ���ҵ�
���ҵ�![]() �ڵ�
�ڵ�![]() ����࣬ͬʱ
����࣬ͬʱ![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]()
��1�������⣺![]() ______��
______��![]() ______��
______��![]() ______��
______��
��2������![]() ���������˶�ʱ����
���������˶�ʱ����![]() ��
��![]() ��
��![]() �������֮�͵���СֵΪ______��
�������֮�͵���СֵΪ______��
��3������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() �����Ḻ���������˶�ͬʱ��������
�����Ḻ���������˶�ͬʱ��������![]() ���ٶ���ÿ��
���ٶ���ÿ��![]() ����λ���ȣ���
����λ���ȣ���![]() ���ٶ���ÿ��2����λ���ȣ����˶������
���ٶ���ÿ��2����λ���ȣ����˶������![]() ��
��
��4������������һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ��
��![]() ����ľ���֮�͵���10����ֱ��д�����еĵ�
����ľ���֮�͵���10����ֱ��д�����еĵ�![]() ��Ӧ������������˵�����ɣ�
��Ӧ������������˵�����ɣ�
���𰸡���1��-1��5��-2����2��6����3���˶�![]() ���
���![]() ��ʱ��
��ʱ��![]() ����4��2��
����4��2��![]() ��
��
��������
��1�����ݾ���ֵ�ķǸ��Լ������a��b��ֵ��Ȼ�����BC�ij���B��C�����λ�ü������c��
��2�������AB�ij���Ȼ�����M���������ϵ�λ�÷������ۣ��ֱ���Ӧ��ͼ�Σ�Ȼ��������ἴ�ɽ��
��3����t��ʱ��![]() �����ݵ�P����Q�ڵ�O�IJ�ͬλ�÷������ۣ��ֱ�ͼ�Σ��ú�ʱ��t��ʽ�ӱ�ʾP��Q�˶���·�̣�Ȼ�������������֪��ʽ�г����̼������t��
�����ݵ�P����Q�ڵ�O�IJ�ͬλ�÷������ۣ��ֱ�ͼ�Σ��ú�ʱ��t��ʽ�ӱ�ʾP��Q�˶���·�̣�Ȼ�������������֪��ʽ�г����̼������t��
��4�����N��Ӧ����Ϊx��Ȼ�����N���������ϵ�λ�÷������ۣ��ֱ���Ӧ��ͼ�Σ�Ȼ���������������ľ��빫ʽ�ֱ��ú�x��ʽ�ӱ�ʾ��NA��NB��NC���ٸ�����֪�����з��̼������N��Ӧ������
�⣺��1����![]() ��
��![]()
��![]()
��ã�![]() ��
��![]() ��
��
�ߵ�![]() �ڵ�
�ڵ�![]() ����࣬
����࣬![]()
��![]()
�ʴ�Ϊ��-1��5��-2��
��2�����������֪��AB=5����-1��=6
�ٵ���M�ڵ�A���ʱ������ͼ��ʾ
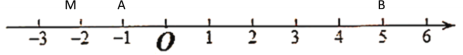
�������֪����ʱMA��MB��AB=6��
�ڵ���M���߶�AB��ʱ������ͼ��ʾ
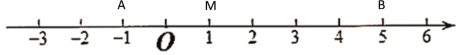
�������֪����ʱMA��MB=AB=6��
�۵���M�ڵ�B�Ҳ�ʱ������ͼ��ʾ
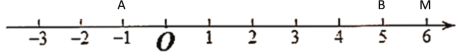
�������֪����ʱMA��MB��AB=6��
����������MA��MB��6
���![]() ��
��![]() ��
��![]() �������֮�͵���СֵΪ6��
�������֮�͵���СֵΪ6��
��3����t��ʱ��![]() �������������
�������������
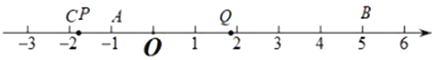
��i������![]() �ڵ�
�ڵ�![]() ����࣬��
����࣬��![]() �ڵ�
�ڵ�![]() ���Ҳ�ʱ������ʾ��ͼ��
���Ҳ�ʱ������ʾ��ͼ��
�����⣺![]() ��
��![]()
��![]()
��![]()
��ã�![]()
�൱![]() ʱ��
ʱ��![]()
����������![]() ��
��![]() �����ڵ�
�����ڵ�![]() �����ʱ������ͼ��ʾ
�����ʱ������ͼ��ʾ
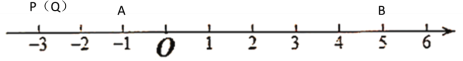
��![]() �����
�����![]() ��
��![]() �غϣ���
�غϣ���![]()
��ʱ![]()
��![]()
��ã�![]()
������������![]() ���
���![]() ��ʱ��
��ʱ��![]()
���˶�![]() ���
���![]() ��ʱ��
��ʱ��![]() ��
��
��4�����N��Ӧ����Ϊx���������������
������N�ڵ�C���ʱ����x��-2ʱ������ͼ��ʾ��
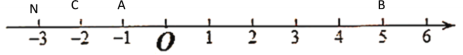
��ʱNC=-2��x��NA=-1��x��NB=5��x
���������֪��NA��NB��NC=10
����-1��x����5��x����-2��x��=10
��ã�x=![]() ��
��
������N�ڵ�C�͵�A֮��ʱ����-2��x��-1ʱ������ͼ��ʾ��

��ʱNC=x����-2��=x��2��NA=-1��x��NB=5��x
���������֪��NA��NB��NC=10
����-1��x����5��x����x��2��=10
��ã�x=![]() ��������ǰ������������ȥ��
��������ǰ������������ȥ��
������N�ڵ�A�͵�B֮��ʱ����-1��x��5ʱ������ͼ��ʾ��
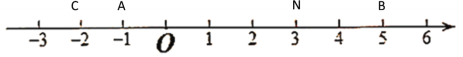
��ʱNC=x����-2��=x��2��NA= x����-1��=x��1��NB=5��x
���������֪��NA��NB��NC=10
����x��1����5��x����x��2��=10
��ã�x=![]() ��
��
������N�ڵ�B�Ҳ�ʱ����x��5ʱ������ͼ��ʾ��
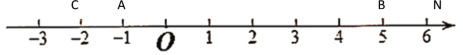
��ʱNC=x����-2��=x��2��NA= x����-1��=x��1��NB= x��5
���������֪��NA��NB��NC=10
����x��1����x��5����x��2��=10
��ã�x=![]() ��������ǰ������������ȥ��
��������ǰ������������ȥ��
�������������еĵ�![]() ��Ӧ������2��
��Ӧ������2��![]() ��
��