题目内容
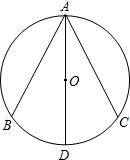 如图,已知AB、AC是⊙O的两条弦,且∠BAC的平分线AD恰好经过圆心O.求证:AB=AC.
如图,已知AB、AC是⊙O的两条弦,且∠BAC的平分线AD恰好经过圆心O.求证:AB=AC.
解:连接BD,CD,
∵AD为直径,
∴∠B=∠C=90°,
∵AD平分∠BAC,
∴BD=CD,
∴在Rt△ABD和Rt△ACD中,
 ,
,
∴Rt△ABD≌Rt△ACD(HL),
∴AB=AC.
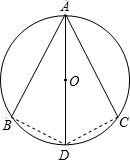
分析:连接BD,CD,根据圆周角定理推出∠B=∠C=90°,再由AD平分∠BAC,即可推出BD=CD,通过求证△ABD≌△ACD,然后根据全等三角形的性质即可推出结论.
点评:本题主要考查圆周角定理,直角三角形全等的判定定理,角平分线的性质,关键在于正确的做出辅助线构建直角三角形.
∵AD为直径,
∴∠B=∠C=90°,
∵AD平分∠BAC,
∴BD=CD,
∴在Rt△ABD和Rt△ACD中,
 ,
,∴Rt△ABD≌Rt△ACD(HL),
∴AB=AC.

分析:连接BD,CD,根据圆周角定理推出∠B=∠C=90°,再由AD平分∠BAC,即可推出BD=CD,通过求证△ABD≌△ACD,然后根据全等三角形的性质即可推出结论.
点评:本题主要考查圆周角定理,直角三角形全等的判定定理,角平分线的性质,关键在于正确的做出辅助线构建直角三角形.

练习册系列答案
相关题目
 16、如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E.
16、如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E.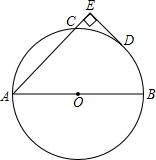 如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.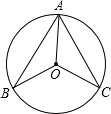 如图,已知AB、AC是⊙O的两条弦,且AB=AC,若∠BOC=100°,则∠BAO=
如图,已知AB、AC是⊙O的两条弦,且AB=AC,若∠BOC=100°,则∠BAO= (2008•宝山区二模)如图,已知AB、AC是⊙O的两条切线,切点分是点B、点C,∠BAC=60°,又⊙O的半径为2cm,则点A与点O的距离为
(2008•宝山区二模)如图,已知AB、AC是⊙O的两条切线,切点分是点B、点C,∠BAC=60°,又⊙O的半径为2cm,则点A与点O的距离为 如图,已知AB:AC=AD:AE,∠BAD=∠CAE.求证:∠ABC=∠ADE.
如图,已知AB:AC=AD:AE,∠BAD=∠CAE.求证:∠ABC=∠ADE.