题目内容
如图,在△ABC中,AB=5,AC=9,S△ABC=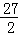 ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点( Q点除外)落在正方形QCGH的边上,请直接写出t的值.
Q点除外)落在正方形QCGH的边上,请直接写出t的值.
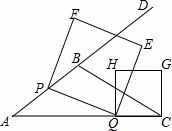
解:(1)如图1,过点B作BM⊥AC于点M,
∵AC=9,S△ABC= ,
,
∴ AC•BM=
AC•BM= ,即
,即 ×9•BM=
×9•BM= ,
,
解得BM=3.
由勾股定理,得
AM= =
= =4,
=4,
则tanA= =
= ;
;
(2)存在.
如图2,过点P作PN⊥AC于点N.
依题意得AP=CQ=5t.
∵tanA= ,
,
∴AN=4t,PN=3t.
∴QN=AC﹣AN﹣CQ=9﹣9t.
根据勾股定理得到:PN2+NQ2=PQ2,
S正方形PQEF=PQ2=(3t)2+(9﹣9t)2=90t2﹣162t+81(0<t< ).
).
∵﹣ =
= =
= 在t的取值范围之内,
在t的取值范围之内,
∴S最小值= =
= =
= ;
;
(3)
①如图3,当点E在边HG上时,t1= ;
;
②如图4,当点F在边HG上时,t2=
 ;
;
③如图5,当点P边QH(或点E在QC上)时,t3=1
④如图6,当点F边C上时,t4= .
.



练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
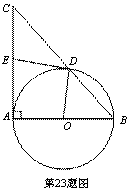

 图象的一个交点.
图象的一个交点.

 中,自变量x的取值范围是
中,自变量x的取值范围是  的结果是 ( )
的结果是 ( ) (B)
(B) (C)
(C) (D)
(D)
 市所有学生中随机
市所有学生中随机 图②中“科技类”所在扇形的圆心角
图②中“科技类”所在扇形的圆心角 的度数;
的度数;