题目内容
已知A(x1、y1),B(x2,y2)是直线y=-x+2与双曲线 (k≠0)的两个不同交点.
(k≠0)的两个不同交点.
(1)求k的取值范围;
(2)是否存在这样k的值,使得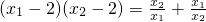 ?若存在,求出这样的k值;若不存在,请说明理由.
?若存在,求出这样的k值;若不存在,请说明理由.
解:(1)∵直线y=-x+2与双曲线 (k≠0)的两个不同交点,-x+2=
(k≠0)的两个不同交点,-x+2= ,
,
即:x2-2x+k=0,
∴△=4-4k>0,
解得:k<1且k≠0;
(2)假设存在k,使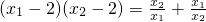 ,
,
∴x1x2-2(x1+x2)+4=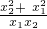 =
=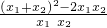 ,
,
∵x1,x2是方程x2-2x+k=0的两根,
∴x1+x2=2,x1x2=k,
∴k-4+4=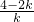 ,
,
解得:k=-1± ,
,
又k<1且k≠0,
∴k=-1- .
.
故存在k=-1- 使得
使得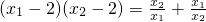 成立.
成立.
分析:(1)直线y=-x+2与双曲线 (k≠0)联立,用△>0即可求出k的取值范围.
(k≠0)联立,用△>0即可求出k的取值范围.
(2)假设存在k,然后根据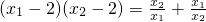 求出k,验证是否符合题意即可.
求出k,验证是否符合题意即可.
点评:本题考查了反比例函数与一次函数的交点,难度较大,关键是用判别式解出k的取值范围后再根据韦达定理进行解答.
 (k≠0)的两个不同交点,-x+2=
(k≠0)的两个不同交点,-x+2= ,
,即:x2-2x+k=0,
∴△=4-4k>0,
解得:k<1且k≠0;
(2)假设存在k,使
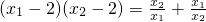 ,
,∴x1x2-2(x1+x2)+4=
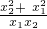 =
=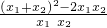 ,
,∵x1,x2是方程x2-2x+k=0的两根,
∴x1+x2=2,x1x2=k,
∴k-4+4=
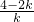 ,
,解得:k=-1±
 ,
,又k<1且k≠0,
∴k=-1-
 .
.故存在k=-1-
 使得
使得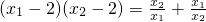 成立.
成立.分析:(1)直线y=-x+2与双曲线
 (k≠0)联立,用△>0即可求出k的取值范围.
(k≠0)联立,用△>0即可求出k的取值范围.(2)假设存在k,然后根据
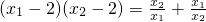 求出k,验证是否符合题意即可.
求出k,验证是否符合题意即可.点评:本题考查了反比例函数与一次函数的交点,难度较大,关键是用判别式解出k的取值范围后再根据韦达定理进行解答.

练习册系列答案
相关题目
已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数y=
的图象上的三点,且x1<x2<0<x3,则y1、y2、y3的大小关系是( )
| 2 |
| x |
| A、y3<y2<y1 |
| B、y1<y2<y3 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
已知A(x1,y1)、B(x2,y2)都是函数y=
(k>0)图象上的点,且x1<x2<0,则y1、y2的大小是( )
| k |
| x |
| A、y1<y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、不能确定 |