Question

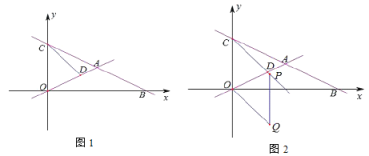
【题目】如图1，在平面直角坐标系中，直线：与：交于点，分别与轴、轴交于点、．

（1）分别求出点、、的坐标；

（2）若是线段上的点，且的面积为12，求直线的函数表达式；

（3）在（2）的条件下，设是射线上的点．

①如图2，过点作，且使四边形为菱形，请直接写出点的坐标；

②在平面内是否存在其它点，使以、、、为顶点的四边形是菱形？若存在，直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）A（6，3）．B（12，0）．C（0，6），（2）y＝x＋6．（3）①Q（3,-3）,②（3，3）,（6,6）.

【解析】

（1）构建方程组确定交点A的坐标，利用待定系数法确定B，C两点坐标即可．

（2）设D（m，m），利用三角形的面积公式，构建方程求出m的值，再利用待定系数法即可解决问题．

（3）①构建OC＝PC，设P（m，m），利用两点间距离公式，构建方程求出m即可．

②当OC为菱形的对角线时，OC垂直平分线段PQ，利用对称性解决问题即可;当PC为对角线时,OQ⊥CP, 利用对称性解决问题即可.

解：（1）由

解得

∴A（6，3）．

∵与分别与x轴、y轴交于点B、C，

∴C（0，6），B（12，0）．

（2）设D（m，m），由题意：OC＝6，△COD的面积为12，

∴×6×m＝12，

∴m＝4，

∴D（4，2），∵C（0，6），

设直线CD的解析式为y＝kx＋b，

则有

解得

∴直线CD的解析式为y＝x＋6．

（3）①∵四边形OCPQ是菱形，

∴OC＝PC＝6，

设P（m，m＋6），

∴m2＋m2＝36，

∴m＝3或3，

∴P（3,-3+6），

∵PQ∥OC，PQ＝OC，

∴Q（3,-3）

②如图，当OC为菱形的对角线时，OC垂直平分线段PQ，

易知P′（3，3），Q′（3，3），

∴满足条件的点Q′的坐标为（3，3）．

（3，3）

如下图,当PC为对角线时,OQ⊥CP,

易知△OCP是等腰直角三角形,

∴四边形OCQP是正方形,此时Q的坐标为（6,6）．