题目内容
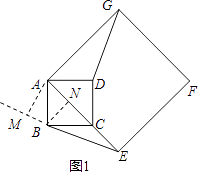
【题目】如图1,正方形ABCD与正方形AEFG的边AB,AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE,DG.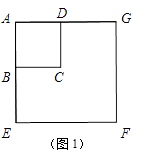
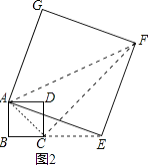
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;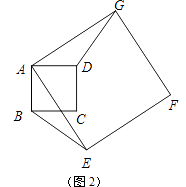
(2)如图3,如果α=45°,AB=2,AE=3 ![]() .
.
①求BE的长;②求点A到BE的距离;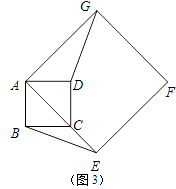
(3)当点C落在直线BE上时,连接FC,直接写出∠FCD的度数.
【答案】
(1)
解:∵四边形ABCD是正方形,
∴AB=AD,∠BAE+∠EAD=90°,
又∵四边形AEFG是正方形,
∴AE=AG,∠EAD+∠DAG=90°,
∴∠BAE=∠DAG.
在△ABE与△ADG中,
∵ 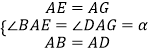 ,
,
∴△ABE≌△ADG(SAS),
∴BE=DG
(2)
解:①如图1,作BN⊥AE于点N,
∵∠BAN=45°,AB=2,
∴AN=BN= ![]() .
.
在△BEN中,
∵BN= ![]() ,NE=3
,NE=3 ![]() ﹣
﹣ ![]() ,
,
∴BE= ![]() ;
;
②如图1,作AM⊥BE于点M,则S△ABE= ![]() AEBN=
AEBN= ![]() ×3
×3 ![]() ×
× ![]() =
= ![]() .
.
又∵S△ABE= ![]() BEAM=
BEAM= ![]() ×
× ![]() ×AM=
×AM= ![]() ,
,
∴AM= ![]() ,即点A到BE的距离
,即点A到BE的距离 ![]()
(3)
解:解:①如图2,连接AC,AF,CF,
∵四边形ABCD与AEFG是正方形,
∴∠ACD=∠AFE=45°,
∵∠DCE=90°
∴点A,C,E,F四点共圆,
∵∠AEF是直角,
∴AF是直径,
∴∠ACF=90°,
∵∠ACD=45°,
∴∠FCD=45°
②如图3,连接AC,AF,FG,CG
由(1)知∵△ABE≌△ADG,
∴∠ABE=∠ADG=90°,
∴DG和CG在同一条直线上,
∴∠AGD=∠AGC=∠BAG,
∵四边形ABCD与AEFG是正方形,
∴∠BAC=∠FAG=45°,
∴∠BAG+∠GAC=45°,∠BAG+∠BAF=45°,
∴∠AGD+∠GAC=45°,
∴∠BAG+∠BAF+∠AGD+∠GAC+∠AGF=180°,
∴点A,C,G,F四点共圆,
∵∠AGF是直角,
∴AF是直径,
∴∠ACF=90°,
∴∠FCD=90°+45°=135°
综上所述,∠FCD的度数为45°或135°.

【解析】(1)根据正方形的性质可得AB=AD,AE=AG,∠BAD=∠EAG=90°,再根据余角的性质,可得∠BAE=∠DAG,然后利用“SAS”证明△ABE≌△ADG,根据全等三角形对应边相等证明即可;(2)①作BN⊥AE于点N,根据勾股定理得出AN=BN= ![]() ,在△BEN中,根据勾股定理即可得出结论;②作AM⊥BE于点M,根据S△ABE=
,在△BEN中,根据勾股定理即可得出结论;②作AM⊥BE于点M,根据S△ABE= ![]() BEAM=3即可得出结论;(3)分两种情况:①E在BC的右边,连接AC,AF,CF,利用点A,C,E,F四点共圆求解,②E在BC的左边,连接AC,AF,FG,CG,首先确定DG和CG在同一条直线上,再利用点A,C,G,F四点共圆求解.
BEAM=3即可得出结论;(3)分两种情况:①E在BC的右边,连接AC,AF,CF,利用点A,C,E,F四点共圆求解,②E在BC的左边,连接AC,AF,FG,CG,首先确定DG和CG在同一条直线上,再利用点A,C,G,F四点共圆求解.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是;
(2)当x=7时,请用列表法或树状图法计算“和为8”的概率;并判断x=7是否可能.







