题目内容
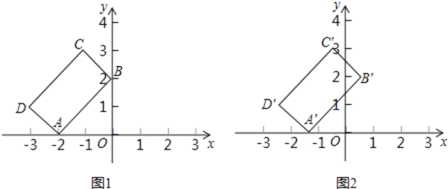
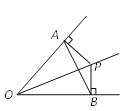
【题目】如图（
），两个不全等的等腰直角三角形
和
叠放在一起，并且有公共的直角顶点
．
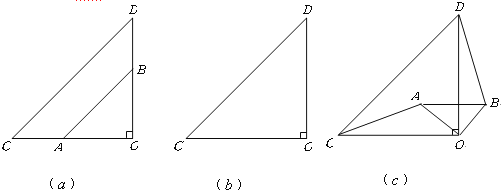
（1）将图（）中的
绕点顺时针旋转
角，在图（
）中作出旋转后的（保留作图痕迹，不写作法，不证明）．
（2）在图（）中，你发现线段
，
的数量关系是 ，直线，相交成 度角．
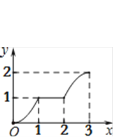
（3）将图（）中的绕点顺时针旋转一个锐角，得到图（
），这时（2）中的两个结论是否成立？作出判断并说明理由．若绕点继续旋转更大的角时，结论仍然成立吗？作出判断，不必说明理由．
【答案】（1）
（2）
；
（3）成立，理由见解析
【解析】
解：（1）如图3（
）
（2）；
（3）成立．如图3（
）
即：
延长
交于，交于
（下面的证法较多）
，
旋转更大角时，结论仍然成立．
（1）旋转的图像与原图形全等，旋转角为
（2）AC=OC-OA,BD=OD-OB,0C=0D,OA=OB,故AC=BD相等，
（3）找出全等的条件即可
练习册系列答案
相关题目
