题目内容
正方形ABCD内有一点P,使△PAB、△PBC、△PCD、△PDA都是等腰三角形,那么具有这样性质的点共有
- A.9个
- B.7个
- C.5个
- D.4个
A
分析:根据正方形的性质可得,满足这样的点首先有:两条对角线的交点;再以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.根据半径相等,这些点就是要求的点.
解答:9个.两条对角线的交点是一个.
以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.
这些点就是要求的点.
故选A.
点评:本题主要考查正方形的性质和等腰三角形的判定的运用,在解答时运用圆的相关性质解答是关键.
分析:根据正方形的性质可得,满足这样的点首先有:两条对角线的交点;再以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.根据半径相等,这些点就是要求的点.
解答:9个.两条对角线的交点是一个.
以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.
这些点就是要求的点.

故选A.
点评:本题主要考查正方形的性质和等腰三角形的判定的运用,在解答时运用圆的相关性质解答是关键.

练习册系列答案
相关题目
 如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为
如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为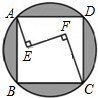 (2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为
(2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为 如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的每个弓形的面积为
如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的每个弓形的面积为