题目内容
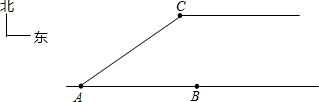 (2012•金山区一模)据新华社12月13日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00巡逻船在A处发现北偏东53.1°方向,相距10海里的C处有一个不明物体正在向正东方向移动,10:15巡逻船在B处又测得该物体位于北偏东18.4°方向的D处.若巡逻船的速度是每小时36海里,
(2012•金山区一模)据新华社12月13日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00巡逻船在A处发现北偏东53.1°方向,相距10海里的C处有一个不明物体正在向正东方向移动,10:15巡逻船在B处又测得该物体位于北偏东18.4°方向的D处.若巡逻船的速度是每小时36海里,(1)试在图中画出点D的大致位置,并求不明物体移动的速度;
(2)假设该不明物体移动的方向和速度保持不变,巡逻船航行的方向和速度也不变,试问什么时间该物体与我巡逻船之间的距离最近?
[备用数据:sin53.1°=0.8,cos53.1°=0.6,cot53.1°=0.75;sin18.4°=0.32,cos18.4°=0.95,cot18.4°=3;].
分析:(1)设10:15时,巡逻船在B处,作北偏东18.4°方向,交过点C的水平线于点D即可;利用53.1°的三角函数值求得AF,CF长,进而求得FB即CG的长,进而利用18.4°的正切值可得GD长,也就求得了CD长,除以时间即为移动的速度;
(2)两者之间的最近距离为直线CD与AB的距离,根据GD和BQ相等可得相应的关系式.
(2)两者之间的最近距离为直线CD与AB的距离,根据GD和BQ相等可得相应的关系式.
解答:解:(1)作AE⊥AB,CF⊥AB于点F,BG⊥CD于点G,由题意,∠EAC=53.1°,∠GBD=18.4°,
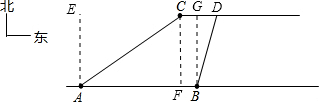
在△CAF中,CF⊥AB,∠ACF=∠EAC=53.1°
∴AF=AC•sin53.1°=10×0.8=8,CF=AC•cos53.1°=10×0.6=6,
∴BG=CF=6
又AB=
×15=9,
∴FB=AB-AF=9-8=1,从而CG=BF=1
在△BDG中,BG⊥CD,∠GBD=18.4°
∵cot18.4°=3,
∴tan18.4°=
∴GD=BG•tan18.4°=6×
=2,
∴CD=CG+GD=1+2=3,3÷
=12(海里/小时),
(2)由题意,不明物体沿CD移动,我巡逻船沿AB运动,且CD∥AB,
∴两者之间的最近距离为直线CD与AB的距离.
设又过了t分钟,不明物体移动到点P,我巡逻船到达点Q,这时PQ⊥AB,
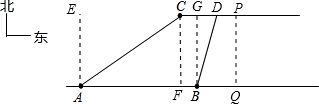
则 DP=
t=
t,BQ=
t=
t,
∴
t+2=
t,解得t=5.
∴10:20两者之间距离最近.

在△CAF中,CF⊥AB,∠ACF=∠EAC=53.1°
∴AF=AC•sin53.1°=10×0.8=8,CF=AC•cos53.1°=10×0.6=6,
∴BG=CF=6
又AB=
| 36 |
| 60 |
∴FB=AB-AF=9-8=1,从而CG=BF=1
在△BDG中,BG⊥CD,∠GBD=18.4°
∵cot18.4°=3,
∴tan18.4°=
| 1 |
| 3 |
∴GD=BG•tan18.4°=6×
| 1 |
| 3 |
∴CD=CG+GD=1+2=3,3÷
| 15 |
| 60 |
(2)由题意,不明物体沿CD移动,我巡逻船沿AB运动,且CD∥AB,
∴两者之间的最近距离为直线CD与AB的距离.
设又过了t分钟,不明物体移动到点P,我巡逻船到达点Q,这时PQ⊥AB,

则 DP=
| 12 |
| 60 |
| 1 |
| 5 |
| 36 |
| 60 |
| 3 |
| 5 |
∴
| 1 |
| 5 |
| 3 |
| 5 |
∴10:20两者之间距离最近.
点评:考查解直角三角形的应用;利用所给角的度数作出相应辅助线,得到直角三角形是解决本题的突破点;利用相应的锐角三角函数求得相关线段长是解决本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目