题目内容
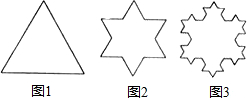
我们来探究“雪花曲线”的有关问题:下图是边长为1的正三角形,将此正三角形的每条边三等分,而以居中的那一条线段为底边再作正三角形,然后以其两腰代替底边,得到第二个图形如下图;再将下图的每条边三等分,并重复上述的作法,得到第三个图形如下图.(1)求第5个图形周长.
(2)求第n个图形与周长C的函数关系式.

分析:(1)注意首先根据前面几个图形找到相邻周长之间的关系.再进一步得到第5个图形周长和第一个图形的周长之间的关系.
(2)根据(1)中分析直接得出规律,依此得出第n个图形与周长C的函数关系式.
(2)根据(1)中分析直接得出规律,依此得出第n个图形与周长C的函数关系式.
解答:解:(1)观察发现:第二个图形在第一个图形的周长的基础上多了它的周长的
.第三个在第二个的基础上,多了其周长的
.依此类推,第二个周长:3×
,
第三个周长:3×
×
,
第四个周长:3×
×
×
.
第五个周长:3×
×
×
×
.
则得到的第5个图形的周长是3×(
)4=
.
(2)n次分形,边长变为原来的(
)n,
∴周长C=3×(
) (n-1),
即第n个图形与周长C的函数关系式为:C=3×(
)n-1.
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
第三个周长:3×
| 4 |
| 3 |
| 4 |
| 3 |
第四个周长:3×
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
第五个周长:3×
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
则得到的第5个图形的周长是3×(
| 4 |
| 3 |
| 256 |
| 27 |
(2)n次分形,边长变为原来的(
| 4 |
| 3 |
∴周长C=3×(
| 4 |
| 3 |
即第n个图形与周长C的函数关系式为:C=3×(
| 4 |
| 3 |
点评:此题考查了平面图形,主要培养学生的观察能力和空间想象能力.读懂题目信息并灵活运用等边三角形的性质是解题的关键.

练习册系列答案
相关题目
 长应等于( )
长应等于( ) 我们来探究“雪花曲线”的有关问题:如图(1)是边长为1的正三角形,将此三正角形的每条边三等分,而以居中的那一条线段为底边再作正三角形;然后以其两腰代替底边,得到第二个图形如图(2);再将图(2)的每条边三等分,并重复上述的作法,得到第三个图形如图(3),如此继续下去,得到的第五个图形的周长应等于
我们来探究“雪花曲线”的有关问题:如图(1)是边长为1的正三角形,将此三正角形的每条边三等分,而以居中的那一条线段为底边再作正三角形;然后以其两腰代替底边,得到第二个图形如图(2);再将图(2)的每条边三等分,并重复上述的作法,得到第三个图形如图(3),如此继续下去,得到的第五个图形的周长应等于 我们来探究“雪花曲线”的有关问题:如图(1)是边长为1的正三角形,将此三正角形的每条边三等分,而以居中的那一条线段为底边再作正三角形;然后以其两腰代替底边,得到第二个图形如图(2);再将图(2)的每条边三等分,并重复上述的作法,得到第三个图形如图(3),如此继续下去,得到的第五个图形的周长应等于______.
我们来探究“雪花曲线”的有关问题:如图(1)是边长为1的正三角形,将此三正角形的每条边三等分,而以居中的那一条线段为底边再作正三角形;然后以其两腰代替底边,得到第二个图形如图(2);再将图(2)的每条边三等分,并重复上述的作法,得到第三个图形如图(3),如此继续下去,得到的第五个图形的周长应等于______.


