��Ŀ����
����������12�֣���ƽ��ֱ������ϵ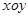 �У���֪���κ���
�У���֪���κ��� ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ���AB=4,��y�ύ�ڵ�C���ҹ���(2,3)��
��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ���AB=4,��y�ύ�ڵ�C���ҹ���(2,3)��
��1����˶��κ����ı���ʽ��
��2���������ߵĶ���ΪD,����CD��CB,�����������Ƿ���ڵ�P,ʹ�á�PBC+��BDC=90��. �����ڣ������P�����ꣻ�������ڣ���˵�����ɣ� ��3����K��������C���ڶԳ���ĶԳƵ㣬��G�������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹA��K��F��G�������ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ������������������F�����ꣻ��������ڣ���˵������
��3����K��������C���ڶԳ���ĶԳƵ㣬��G�������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹA��K��F��G�������ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ������������������F�����ꣻ��������ڣ���˵������
��1�� 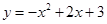 ��
��
��2������,��֤��DC��BC,�ɡ�PBC+��BDC=90��,֪��һ��P,ʹ�á�PBC=��DBC,��֪P������λ��:(1,4)��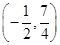
��3������4�������ĵ�F���ֱ���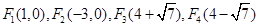
������1�������ߵĶԳ��x=��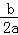 =��
=��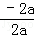 =1����AB=4���� A����1��0����B��3��0����
=1����AB=4���� A����1��0����B��3��0����
�ٴ���㣨2��3���ɵã�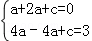 �����
�����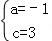
����κ����ı���ʽ��y=��x2+2x+3��
��2���ɣ�1��֪��y=��x2+2x+3=����x��1��2+4���� D��1��4����
BC2=18��CD2=2��BD2=20����BC2+CD2=BD2������BCD��ֱ�������Σ���DC��BC��
���BDC+��DBC=90�㣬����D���ϵ�P��Ҫ��P1��1��4����
�ӳ�DC��E��ʹ��DC=CE�����BDE�ǵ��������Σ��ҡ�DBC=��EBC����ֱ��BE�������ߵĽ���Ҳ���ϵ�P��Ҫ��B����⣩
ͨ��ͼʾ�����ѿ�����D��E���ڵ�C�Գƣ��� E����1��2������ֱ��BE��y=kx+b�����У� �����
�����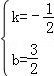
��ֱ��BE��y=�� x+
x+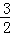 �����������ߵĽ���ʽ�ã�
�����������ߵĽ���ʽ�ã�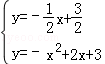 �����
�����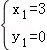 ���ᣩ��
���ᣩ��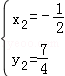
��P2����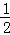 ��
��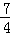 ����
����
���ϣ����ڷ��������ĵ�P��������Ϊ��1��4��������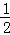 ��
��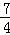 ����
����
��3����֪��K��2��3����
�����⣬A��F����x���ϣ�����ƽ���ı��ε��ص㲻�ѿ�����G��������Ϊ3��3��
��yG=3ʱ����x2+2x+3=3����� x=0��2��
��G��������0��3����
��ʱ��F������Ϊ����1��2��0����1+2��0����������3��0������1��0����
��yG=��3ʱ����x2+2x+3=��3����� x=1��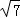 ��
��
��G��������1+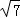 ��0����1��
��0����1��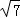 ��0����
��0����
��ʱ��F������Ϊ��4+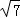 ��0������4��
��0������4��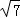 ��0����
��0����
���ϣ����ĸ����������ĵ�F��������Ϊ����3��0������1��0������4+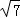 ��0������4��
��0������4��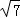 ��0����
��0����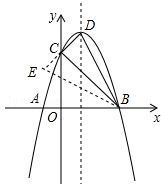


 ��3�����P��x��ľ���Ϊh����ȷ��h��ȡֵ��Χ����˵�����ɡ�
��3�����P��x��ľ���Ϊh����ȷ��h��ȡֵ��Χ����˵�����ɡ� �����㣨0��10��
�����㣨0��10��
 �У���֪���κ���
�У���֪���κ��� ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ���AB=4,��y�ύ�ڵ�C���ҹ���(2,3)��
��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ���AB=4,��y�ύ�ڵ�C���ҹ���(2,3)�� ��3����K��������C���ڶԳ���ĶԳƵ㣬��G�������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹA��K��F��G�������ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ������������������F�����ꣻ��������ڣ���˵������
��3����K��������C���ڶԳ���ĶԳƵ㣬��G�������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹA��K��F��G�������ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ������������������F�����ꣻ��������ڣ���˵������