Question

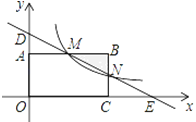
【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标（4，2），过点D（0，3）和E（6，0）的直线分别于AB，BC交于点M，N．

（1）求直线DE的解析式和点M的坐标；

（2）若反比例函数y=（x＞0）的图象经过点M，求该反比函数的解析式，并通过计算判断点N是否在该函数的图象上．

Answer 1

【答案】（1），M（2，2）；（2），在．

【解析】试题分析：（1）设直线DE的解析式为，将D（0，3），E（6，0）代入，解方程即可求出直线DE的解析式；由矩形的性质可得M点与B点纵坐标相等，将y=2代入直线DE的解析式，求出x的值，即可得到M的坐标；

（2）将点M（2，2）代入，即可求出反比函数的解析式，再由直线DE的解析式求出N点坐标，进而判断点N是否在该函数的图象上．

试题解析：（1）设直线DE的解析式为，∵D（0，3），E（6，0），∴，解得： ，∴直线DE的解析式为；当y=2时， ，解得x=2，∴M的坐标为（2，2）；

（2）∵反比例函数（x＞0）的图象经过点M（2，2），∴m=2×2=4，∴该反比函数的解析式是；∵直线DE的解析式为，∴当x=4时，y=×4+3=1，∴N点坐标为（4，1），∵4×1=4，∴点N在函数的图象上．