题目内容

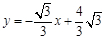在平面直角坐标系xOy中，已知直线l1经过点A(-2，0)和点B(0，)，直线l2的函数表达式为，l1与l2相交于点P．⊙C是一个动圆，圆心C在直线l1上运动，设圆心C的横坐标是a．过点C作CM⊥x轴，垂足是点M．
【小题1】求直线l1的函数表达式；
【小题2】　当⊙C和直线l2相切时，请证明点P到直线CM的距离等于⊙C的半径R，并写出R=时a的值.
【小题3】当⊙C和直线l2不相离时，已知⊙C的半径R=，记四边形NMOB的面积为S(其中点N是直线CM与l2的交点)．S是否存在最大值？若存在，求出这个最大值及此时a的值；若不存在，请说明理由．


【小题1】
【小题2】
【小题3】

解析

练习册系列答案
相关题目
13、在平面直角坐标系xOy中，已知点A（2，-2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的有
4
个．
在平面直角坐标系xOy中，已知抛物线y=ax2+bx+c的对称轴是x=1，并且经过（-2，-5）和（5，-12）两点．
（1）求此抛物线的解析式；
（2）设此抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于C 点，D是线段BC上一点（不与点B、C重合），若以B、O、D为顶点的三角形与△BAC相似，求点D的坐标；
（3）点P在y轴上，点M在此抛物线上，若要使以点P、M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标．
精英家教网如图，在平面直角坐标系xOy中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知|OA|：|OB|=1：5，|OB|=|OC|，△ABC的面积S△ABC=15，抛物线y=ax2+bx+c（a≠0）经过A、B、C三点．
（1）求此抛物线的函数表达式；
（2）设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；
（3）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为7
2
？若存在，求出点M的坐标；若不存在，请说明理由．
在平面直角坐标系xOy中，已知A（2，-2），B（0，-2），在坐标平面中确定点P，使△AOP与△AOB相似，则符合条件的点P共有
5
5
个．
如图，在平面直角坐标系xOy中，A（2，1）、B（4，1）、C（1，3）．与△ABC与△ABD全等，则点D坐标为
（1，-1），（5，3）或（5，-1）
（1，-1），（5，3）或（5，-1）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网