题目内容
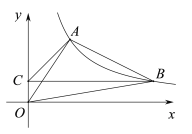
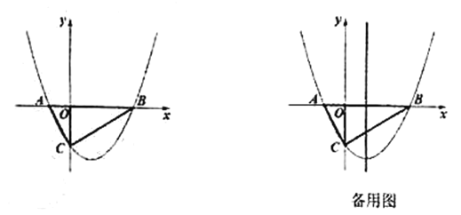
【题目】在平面直角坐标系中,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 得
得![]() ,
,![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
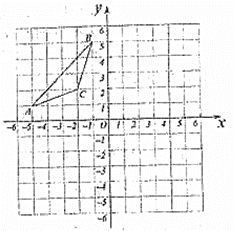
(1)画出![]() 和
和![]() ;
;
(2)![]() ______;
______;
(3)![]() 与
与![]() 组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
【答案】(1)见解析;(2)![]() ;(3)是轴对称图形,对称轴所在的直线解析式是
;(3)是轴对称图形,对称轴所在的直线解析式是![]() ,
,![]() .
.
【解析】
(1)根据旋转的性质,旋转不改变图形的大小和形状,结合题意根据三角形全等可得答案,(2)对于三角函数值得求解,要找到对应的直角三角形,通过网格长度求出即可,
(3)先找到对称轴所在直线,根据点的坐标求出一次函数的解析式即可
解:(1)如图:

(2)作CD⊥AB,由题可知AC=BC=![]() ,故△ABC为等腰三角形,则D为AB的中点,
,故△ABC为等腰三角形,则D为AB的中点,
∵AB=![]() ,则AD=
,则AD=![]() ,
,
根据勾股定理可得CD=![]() ,∴
,∴![]()
![]() =
=![]() ;
;
(3)是轴对称图形,有图可以观察得出对称轴所在的直线为CC2,或者OC1直线,C(-2,2),C2(2,-2),C1(2,2),分别代入解出解析式是![]() ,
,![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目