题目内容
设关于x的方程4x2-4(a+2)x+a2+11=0的两根为x1、x2,若x1-x2=3,则a的值是________
4
分析:由根与系数的关系得到两根和与两根积,再由完全平方公式进行计算求出a的值,同时求出的a值必须使判别式大于0.
解答:根据根与系数的关系有:
x1+x2=a+2,x1x2= ,
,
x1-x2=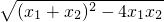 =
= =3
=3
a2+4a+4-a2-11=9
a=4
∵△=16(a+2)2-16(a2+11)>0
∴a> .
.
∴a=4符合题意.
故答案是:4.
点评:本题考查的是一元二次方程根与系数的关系,根据根与系数的关系得到两根和与两根积,运用完全平方公式,代入两根之差求出a的值.
分析:由根与系数的关系得到两根和与两根积,再由完全平方公式进行计算求出a的值,同时求出的a值必须使判别式大于0.
解答:根据根与系数的关系有:
x1+x2=a+2,x1x2=
 ,
,x1-x2=
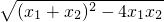 =
= =3
=3a2+4a+4-a2-11=9
a=4
∵△=16(a+2)2-16(a2+11)>0
∴a>
 .
.∴a=4符合题意.
故答案是:4.
点评:本题考查的是一元二次方程根与系数的关系,根据根与系数的关系得到两根和与两根积,运用完全平方公式,代入两根之差求出a的值.

练习册系列答案
相关题目
 ?
? ?
?