题目内容
如图,一抛物线与x轴相交于A、B两点,与y轴正半轴交于点C,对称轴x= 与x轴相交于点
与x轴相交于点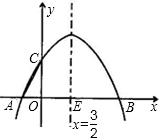 E,且OC=2,tan∠ACO=
E,且OC=2,tan∠ACO= .
.
(1)求抛物线的解析式;
(2)在对称轴上找一点D,使△ADC周长最短,求此时线段DE的长;
(3)探究:在(1)中抛物线上是否存在点P,使PB=PC?若存在,求出P的坐标,请说明理由.
 解:(1)在Rt△ACO中,
解:(1)在Rt△ACO中,∵OC=2,tan∠ACO=
 ,
,∴OA=1,∴A(-1,0),C(0,2),
由对称性易知B(4,0)
∴设过A、B、C三点的解析式为y=a(x-x1)(x-x2),
∴2=a(0+1)(0-4),
解得a=-
 ,
,∴y=-
 (x+1)(x-4)=-
(x+1)(x-4)=- x2+
x2+ x+2;
x+2;(2)连接BC交对称轴x=
 于一点D.
于一点D.∵点A、B关于x=
 对称,
对称,∴D点即为所求的点,
连接AD,此时△ADC的周长最短;
∵OE=
 ,OB=4,
,OB=4,∴BE=
 ,
,∵DE∥CO,易证:△BDE∽△BCO,
∴
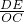 =
=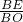 即
即 =
=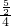 ,
,∴DE=
 ;
;(3)存在.
设F为BC的中点,则点P为直线EF与抛物线的交点,可求得F(2,1),
∴直线EF的解析式为:y=2x-3,
由2x-3=-
 x2+
x2+ +2,
+2,解得x1=
 ,x2=
,x2= ,
,∴符合条件的点P的坐标为:
P1(
 ,-4+
,-4+ ),P2(
),P2( ,-4-
,-4- ).
).分析:(1)根据题意可得出A、C两点的坐标,由对称性易知点B的坐标,设过A、B、C三点的解析式,代入数据即可得出解析式;
(2)连接BC交对称轴于一点D.可求得BE的长,由平行线的性质进而得出DE的长;
(3)先下结论,再设F为BC的中点,则点P为直线EF与抛物线的交点,可求得F的坐标,得出EF的解析式,根据交点坐标的求法即可得出答案.
点评:本题是一道二次函数的综合题,考查了用待定系数法求二次函数的解析式、一元二次方程的解法,综合性较强,难度较大.

练习册系列答案
相关题目
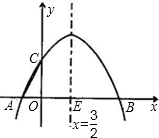 E,且OC=2,tan∠ACO=
E,且OC=2,tan∠ACO=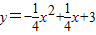 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.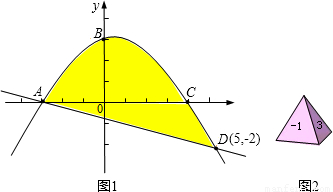
 与x轴相交于点E,且OC=2,tan∠ACO=
与x轴相交于点E,且OC=2,tan∠ACO= .
.
 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.