题目内容
已知关于x的一元二次方程x2-3x-k=0有两个实数根为x1,x2.(x1≤x2)
(1)求k的取值范围;
(2)试用含k的代数式表示x1与x2.
(3)当 时.求k的值.
时.求k的值.
解:(1)由根的判别式,得
(-3)2+4k≥0
∴k≥- ;
;
(2)∵a=1,b-3,c=-k,
∴b2-4ac=(-3)2+4k,
∴ ;
;
(3)由根与系数的关系,得
x1+x2=3,x1x2=-k,
∵ ,
,
∴(x2+x1)(x2-x1)=3
∵ ,
,
∴x2-x1=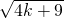 ,
,
∴3•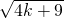 =3,
=3,
∴k=-2
分析:(1)利用根的判别式就可以直接求出k的取值范围.
(2)用求根公式法解这个二元一次方程就可以把x1、x2表示出来.
(3)利用根与系数的关系就可以表示出x1+x2=3,x1x2=-k,再条件及通过变形就可以求出k的值.
点评:本题考查了根的判别式的运用,根与系数的关系的运用,公式法解二元一次方程的运用.
(-3)2+4k≥0
∴k≥-
 ;
;(2)∵a=1,b-3,c=-k,
∴b2-4ac=(-3)2+4k,
∴
 ;
;(3)由根与系数的关系,得
x1+x2=3,x1x2=-k,
∵
 ,
,∴(x2+x1)(x2-x1)=3
∵
 ,
,∴x2-x1=
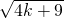 ,
,∴3•
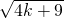 =3,
=3,∴k=-2
分析:(1)利用根的判别式就可以直接求出k的取值范围.
(2)用求根公式法解这个二元一次方程就可以把x1、x2表示出来.
(3)利用根与系数的关系就可以表示出x1+x2=3,x1x2=-k,再条件及通过变形就可以求出k的值.
点评:本题考查了根的判别式的运用,根与系数的关系的运用,公式法解二元一次方程的运用.

练习册系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.