题目内容
 如图,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).
如图,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).(1)求该抛物线的表达式,并写出该抛物线的顶点坐标;
(2)在x轴的正半轴上是否存在点P,使得△PAB是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)根据抛物线y=-x2+bx+c过点A(4,0)、B(1,3)列出关于b和c的二元一次方程组,求出b和c,抛物线解析式求出,顶点坐标即可求出;
(2)假设存在P(a,0),分三种情况进行讨论,①当PB=PA时,②当PB=BA时,③当PA=AB时,分别求出满足△PAB是等腰三角形时a的值.
(2)假设存在P(a,0),分三种情况进行讨论,①当PB=PA时,②当PB=BA时,③当PA=AB时,分别求出满足△PAB是等腰三角形时a的值.
解答:解:(1)∵抛物线y=-x2+bx+c过点A(4,0)、B(1,3),
∴
,
∴
,
∴抛物线的表达式y=-x2+4x=-(x-2)2+4,
∴抛物线的顶点坐标为(2,4),
(2)假设存在P(a,0),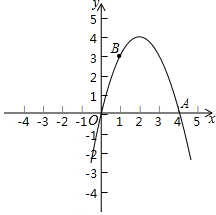
①当PB=PA时,
=|4-a|,
解得a=1,
此时P点坐标为(1,0),
②当PB=BA时,
=
,
解得a=-2,
此时P点坐标为(-2,0),
③当PA=AB时,
|a-4|=3
,
解得a=4+3
或a=4-3
,
此时P点坐标为(4+3
,0)或(4-3
,0),
综上所述,满足条件P的坐标(1,0)、(-2,0)、(4+3
,0)或(4-3
,0).
∴
|
∴
|
∴抛物线的表达式y=-x2+4x=-(x-2)2+4,
∴抛物线的顶点坐标为(2,4),
(2)假设存在P(a,0),

①当PB=PA时,
| (1-a)2+32 |
解得a=1,
此时P点坐标为(1,0),
②当PB=BA时,
| (1-a)2+32 |
| 32+(1-4)2 |
解得a=-2,
此时P点坐标为(-2,0),
③当PA=AB时,
|a-4|=3
| 2 |
解得a=4+3
| 2 |
| 2 |
此时P点坐标为(4+3
| 2 |
| 2 |
综上所述,满足条件P的坐标(1,0)、(-2,0)、(4+3
| 2 |
| 2 |
点评:本题主要考查二次函数的综合题,解答本题的关键是正确求出函数的解析式,解答第二问的时候需要分三种情况进行讨论,同学们很容易出现漏解的情况,请同学们解答的时候稍加注意.

练习册系列答案
相关题目
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
