题目内容
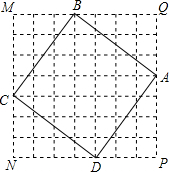
如图，正方形MNPQ的顶点在三角形ABC的边上，当边BC=a与高AD=h满足什么条件时，正方形MNPQ的面积是三角形ABC面积的一半？
分析：设正方形的边长是x，由相似三角形得
=
，解得x=
．根据题意(
) 2=
ah，化简得（a-h）2=0；即AD=BC（也可以观察△ADC中只有当P是AC中点时，矩形面积是三角形面积的一半，这时P、Q是AC、AB的中点））．
| x |
| a |
| h-x |
| h |
| ah |
| a+h |
| ah |
| a+h |
| 1 |
| 4 |
解答：解：当a=h时，正方形面积是原三角形面积的一半，
设正方形的边长是x，由△AQP∽△ABC得
=
，
解得x=
．根据题意(
) 2=
ah，
化简得（a-h）2=0；即AD=BC．
∴当a=h时，正方形面积是原三角形面积的一半，
设正方形的边长是x，由△AQP∽△ABC得
| x |
| a |
| h-x |
| h |
解得x=
| ah |
| a+h |
| ah |
| a+h |
| 1 |
| 4 |
化简得（a-h）2=0；即AD=BC．
∴当a=h时，正方形面积是原三角形面积的一半，
点评：此题主要考查学生对相似三角形的判定与性质这一知识点的理解和掌握，解答此题的关键是利用相似三角形的相比．属于中档题．
练习册系列答案
相关题目
学公式或定理吗？相信你能给出简明的推理过程．
如图，正方形MNPQ的边长为1，正方形ABCD的边长为2，点M与点A重合，点N在线段AB上，点P在正方形内部，正方形MNPQ沿正方形ABCD的边按A→B→C→D→A→…方向滚动，始终保持M、N、P、Q四点在正方形内部或边界上，直到正方形回到初始位置为止．则P经过的最短路程为
的方向滚动，
直至△MNP中有一个点与点B重合为止，则点P经过
