题目内容
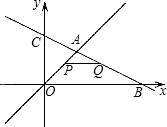
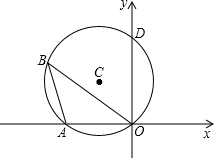 如图,⊙C经过坐标原点,并与坐标轴分别交于A、D两点,点B在⊙C上,∠B=30°,点D的坐标为(0,2),求A、C两点的坐标.
如图,⊙C经过坐标原点,并与坐标轴分别交于A、D两点,点B在⊙C上,∠B=30°,点D的坐标为(0,2),求A、C两点的坐标.
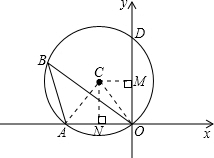 解:连接AC、OC,过点C分别作CM⊥OD于M,CN⊥OA于N.
解:连接AC、OC,过点C分别作CM⊥OD于M,CN⊥OA于N.∵点B在⊙C上,∠B=30°,
∴∠ACO=60°.
∵CA=CO,
∴△CAO是等边三角形.
∴CA=CO=OA,∠COA=60°.
∴∠COM=30°.
∵CM⊥OD,点C为圆心,点D的坐标为(0,2),
∴
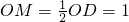 .
.在Rt△OCM中,
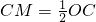 ,
,由勾股定理得,
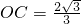 .
.∴
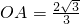 .
.同理可得
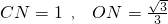 .
.∴点A的坐标为
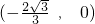 .
.点C的坐标为
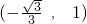 .
.分析:分别连接AC,OC,要求C点的坐标,故过点C分别向x,y轴作垂线交x轴于N点,交y轴于点M,根据题意,又∠B=30°,根据圆周角和圆心角之间的关系,可知∠ACO=60°,即△CAO是等边三角形.已知点D的坐标为(0,2),可知OM=1,根据勾股定理即可得出OC和CM的长,点C的坐标,又OA=OC,且点A位于x轴上,可得点的坐标.
点评:本题考查了圆周角和圆心角中间的关系和垂径定理在坐标系中的运用.

练习册系列答案
相关题目
 条件是
条件是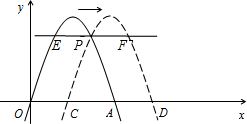 右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P
右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),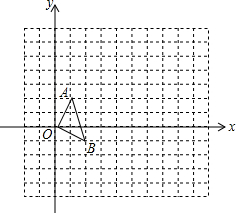 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
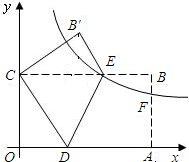 如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、BC边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、BC边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.