题目内容
(本题满分12分)如图1,△ABC的边BC在直线上,AC⊥BC,且AC=BC;△EFP的边FP也在直线
上,边EF与边AC重合,且EF=FP.
1.(1)将△EFP沿直线向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
2.(2)将△EFP沿直线向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
3.(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.
1.(1)BQ=AP……1分 证出△BCQ≌△ACP……………3分 得出BQ=AP……4分
2.(2)BQ=AP……5分 证出△BCQ≌△ACP……………7分 得出BQ=AP……8分
3.(3)当0≤x<4时,………………………………………………9分
当4≤x≤8时,………………………………………………10分
当0≤x<4时,x=时,S的最大值为
;当4≤x≤8时,x=4时,S的最大值为4.
∴当x=时,S的最大值为
…………………………………………………12分
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
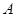 作
作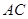 ∥
∥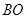 交上述函数图像于点
交上述函数图像于点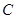 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)

 的长;
的长;
 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?

 ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
 时,求线段
时,求线段 的长;
的长; 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.