题目内容
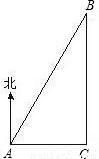
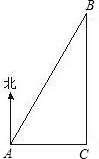 一艘轮船从西向东航行,上午10时航行到点A处,此时测得在船北偏东30°上有一灯塔B,到11时测得灯塔B正好在船的正北方向,此时轮船所处位置为C点(如图),若该船的航行速度为每小时20海里,那么船在C点时距离灯塔B多远?(
一艘轮船从西向东航行,上午10时航行到点A处,此时测得在船北偏东30°上有一灯塔B,到11时测得灯塔B正好在船的正北方向,此时轮船所处位置为C点(如图),若该船的航行速度为每小时20海里,那么船在C点时距离灯塔B多远?( 取1.73)
取1.73)
解:由题意知∠BAC=60°,∠C=90°,
AC=20×(11-10)=20(海里).
∴tan∠BAC= ,即tan60°=
,即tan60°= .
.
∴BC=20tan60°=20 ≈34.6(海里).
≈34.6(海里).
分析:本题是求BC的长,在直角三角形ABC中,AB的长可根据路程=速度×时间求出,又知道了∠BAC的度数,那么BC就能求出来了.
点评:本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.
AC=20×(11-10)=20(海里).
∴tan∠BAC=
 ,即tan60°=
,即tan60°= .
.∴BC=20tan60°=20
 ≈34.6(海里).
≈34.6(海里).分析:本题是求BC的长,在直角三角形ABC中,AB的长可根据路程=速度×时间求出,又知道了∠BAC的度数,那么BC就能求出来了.
点评:本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
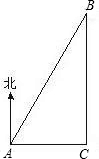 一艘轮船从西向东航行,上午10时航行到点A处,此时测得在船北偏东30°上有一灯塔B,到11时测得灯塔B正好在船的正北方向,此时轮船所处位置为C点(如图),若该船的航行速度为每小时20海里,那么船在C点时距离灯塔B多远?(
一艘轮船从西向东航行,上午10时航行到点A处,此时测得在船北偏东30°上有一灯塔B,到11时测得灯塔B正好在船的正北方向,此时轮船所处位置为C点(如图),若该船的航行速度为每小时20海里,那么船在C点时距离灯塔B多远?(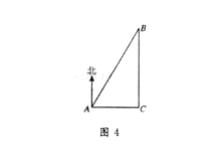
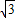 取1.73)
取1.73)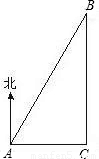
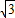 取1.73)
取1.73)