题目内容
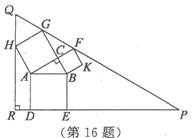
 勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是
勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是60
60
.分析:根据勾股定理求出AB,求出△ACB≌△BOG≌△GHM,求出AC=OB=HG=4,BC=OG=MH=3,分别求出长方形FHNR,正方形BCDE,正方形ACQP,正方形ABGM的面积,即可求出答案.
解答:解:如图,在Rt△ABC中,BC=3,AC=4,则根据勾股定理得到AB=
=5.
延长CB交FH于O,
∵四边形ABGM,APQC,BCDE均为正方形,
∴BG=AB=GM,∠ACB=∠ABG=∠F=∠H=∠MGB=90°,BC∥DE,
∴∠BOG=∠F=90°,
∴∠CAB+∠ABC=90°,∠ABC+∠GBO=180°-90°=90°,
∴∠CAB=∠GBO,
在△ACB和△BOG中,
,
∴△ACB≌△BOG(AAS),
∴AC=OB=4,OG=BC=3,
同理可证△MHG≌△GOB,
∴MH=OG=3,HG=OB=4,
∴FR=4+3+4=11,FH=3+3+4=10,
∴S空白=S长方形HFRN-S正方形BCDE-S正方形ACQP-S正方形ABGM
=11×10-3×3-4×4-5×5=60,
故答案为:60.
| AC2+BC2 |

延长CB交FH于O,
∵四边形ABGM,APQC,BCDE均为正方形,
∴BG=AB=GM,∠ACB=∠ABG=∠F=∠H=∠MGB=90°,BC∥DE,
∴∠BOG=∠F=90°,
∴∠CAB+∠ABC=90°,∠ABC+∠GBO=180°-90°=90°,
∴∠CAB=∠GBO,
在△ACB和△BOG中,
|
∴△ACB≌△BOG(AAS),
∴AC=OB=4,OG=BC=3,
同理可证△MHG≌△GOB,
∴MH=OG=3,HG=OB=4,
∴FR=4+3+4=11,FH=3+3+4=10,
∴S空白=S长方形HFRN-S正方形BCDE-S正方形ACQP-S正方形ABGM
=11×10-3×3-4×4-5×5=60,
故答案为:60.
点评:本题考查了正方形性质,全等三角形的性质和判定,勾股定理的应用,关键是求出长方形HFRN的边长.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
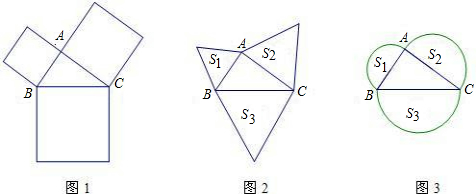
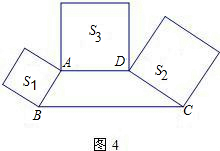 梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的数量关系式为
梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的数量关系式为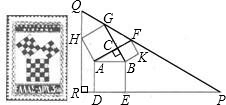
 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在上图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=8.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,那么△PQR的周长等于
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在上图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=8.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,那么△PQR的周长等于