��Ŀ����
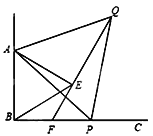
����Ŀ����ͼ��������y=ax2+bx��2�ĶԳ�����ֱ��x=1����x�ύ��A��B���㣬��y�ύ�ڵ�C����A������Ϊ����2��0������PΪ�������ϵ�һ�����㣬����P��PD��x���ڵ�D����ֱ��BC�ڵ�E��
��1���������߽���ʽ��
��2������P�ڵ�һ�����ڣ���OD=4PEʱ�����ı���POBE�������
��3���ڣ�2���������£�����MΪֱ��BC��һ�㣬��NΪƽ��ֱ������ϵ��һ�㣬�Ƿ���������ĵ�M�͵�N��ʹ���Ե�B��D��M��NΪ������ı��������Σ������ڣ�ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) �����߽���ʽΪy=![]() x2��
x2��![]() x��2��(2)
x��2��(2)![]() ;(3) ��N��
;(3) ��N��![]() ����
����![]() ����4.6��
����4.6��![]() ����5��
����5��![]() ����
����![]() ����5+
����5+![]() ��
��![]() �����Ե�B��D��M��NΪ������ı��������Σ�
�����Ե�B��D��M��NΪ������ı��������Σ�
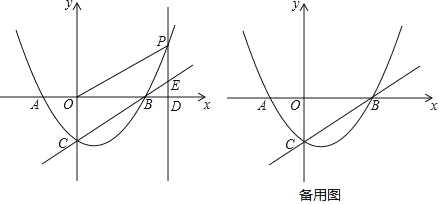
�������������������1����������![]() �ĶԳ�����ֱ��x=1��A����2��0�����������ϣ������з��̼��ɵõ����ۣ�
�ĶԳ�����ֱ��x=1��A����2��0�����������ϣ������з��̼��ɵõ����ۣ�
��2�����ݺ�������ʽ�õ�B��4��0����C��0����2�������BC�Ľ���ʽ����D��m��0�����õ�E��m��![]() ����P��m��
����P��m��![]() ����������֪�����з��̵õ�m=5��m=0����ȥ�������D��P��E�����꣬���������ε������ʽ���ɵõ����ۣ�
����������֪�����з��̵õ�m=5��m=0����ȥ�������D��P��E�����꣬���������ε������ʽ���ɵõ����ۣ�
��3����M��n��![]() ��������BDΪ�Խ��ߣ��������ε����ʵõ�MN��ֱƽ��BD�����n��ֵ�����ǵõ�N������������BDΪ�ߣ��������ε����ʵõ�MN��BD��MN=BD=MD=1����M��MH��x����H�����ݹ��ɶ����з��̼��ɵõ����ۣ�
��������BDΪ�Խ��ߣ��������ε����ʵõ�MN��ֱƽ��BD�����n��ֵ�����ǵõ�N������������BDΪ�ߣ��������ε����ʵõ�MN��BD��MN=BD=MD=1����M��MH��x����H�����ݹ��ɶ����з��̼��ɵõ����ۣ�
�����������1����������![]() �ĶԳ�����ֱ��x=1��A����2��0�����������ϣ�
�ĶԳ�����ֱ��x=1��A����2��0�����������ϣ�
�� ����ã�
����ã�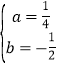 ��
��
�������߽���ʽΪ![]() ��
��
��2����![]() =0����ã�x1=��2��x2=4����x=0ʱ��y=��2��
=0����ã�x1=��2��x2=4����x=0ʱ��y=��2��
��B��4��0����C��0����2������BC�Ľ���ʽΪy=kx+b������![]() ����ã�
����ã�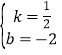 ��
��
��![]() ��
��
��D��m��0������DP��y�ᣬ
��E��m��![]() ����P��m��
����P��m��![]() ����
����
��OD=4PE��
��m=4��![]() ��
��![]() ��
��
��m=5��m=0����ȥ����
��D��5��0����P��5��![]() ����E��5��
����E��5��![]() ����
����
���ı���POBE�����=S��OPD��S��EBD=![]() ��5��
��5��![]() ��
��![]() ��1��
��1��![]() =
=![]() ��
��
��3�����ڣ���M��n��![]() ����
����
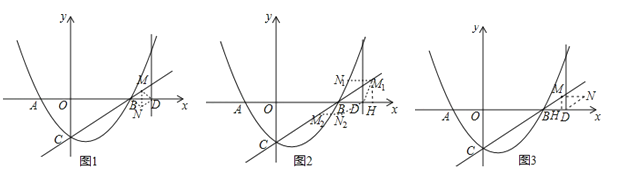
����BDΪ�Խ��ߣ���ͼ1��
���ı���BNDM�����Σ�
��MN��ֱƽ��BD��
��n=4+![]() =
=![]() ��
��
��M��![]() ��
��![]() ����
����
��M��N����x��Գƣ�
��N��![]() ����
����![]() ����
����
����BDΪ�ߣ���ͼ2��
���ı���BNDM�����Σ�
��MN��BD��MN=BD=MD=1��
��M��MH��x����H��
��MH2+DH2=DM2����![]() ��
��
��n1=4���������⣩��n2=5.6��
��N��4.6��![]() ����ͬ��
����ͬ��![]() ��
��
��n1=![]() ���������⣬��ȥ����n2=
���������⣬��ȥ����n2=![]() ��
��
��N��![]() ��
��![]() ����
����
����BDΪ�ߣ���ͼ3����M��MH��x����H��
��MH2+BH2=BM2����![]() ��
��
��n1=![]() ��n2=
��n2=![]() ���������⣬��ȥ����
���������⣬��ȥ����
��N��![]() ��
��![]() ����
����
������������N��![]() ����
����![]() ����4.6��
����4.6��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() �����Ե�B��D��M��NΪ������ı��������Σ�
�����Ե�B��D��M��NΪ������ı��������Σ�

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�