题目内容
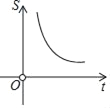
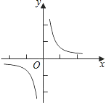
【题目】已知反比例函数![]() 的图象如图所示,点
的图象如图所示,点![]() ,
,![]() 是该图象上的两点.
是该图象上的两点.
(1)求![]() 的取值范围;
的取值范围;
(2)比较![]() 与
与![]() 的大小;
的大小;
(3)若点![]() 在该反比例函数图象上,求此反比例函数的解析式;
在该反比例函数图象上,求此反比例函数的解析式;
(4)若![]() 为第一象限上的一点,作
为第一象限上的一点,作![]() 轴于点
轴于点![]() ,求
,求![]() 的面积(用含
的面积(用含![]() 的式子表示)
的式子表示)
【答案】(1)![]() ;(2)
;(2)![]() ;(3):
;(3):![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据反比例函数的图象在一、三象限即可得出m的取值范围;
(2)根据反比例函数的图象在一、三象限判断出函数图象在每一象限内的增减性,再根据-1>-2即可得出结论;
(3)把点C(3,1)代入反比例函数y=![]() ,求出m的值即可;
,求出m的值即可;
(4)根据反比例函数系数k的几何意义得出结论即可.
(1)∵反比例函数的图象在一、三象限,
![]() ,即
,即![]() ;
;
(2)∵反比例函数的图象在一、三象限,
∴在每一象限内![]() 随
随![]() 的增大而减小,
的增大而减小,
∴![]() ,
,
∴![]() ;
;
(3)∵点![]() 在该反比例函数图象上,
在该反比例函数图象上,
∴![]() ,解得
,解得![]() ,
,
∴此函数的解析式为:![]() ;
;
(4)∵![]() 为第一象限上的一点,
为第一象限上的一点,![]() 轴于点
轴于点![]() ,
,
∴![]() .
.

练习册系列答案
相关题目