题目内容
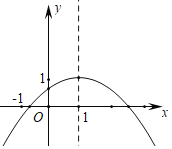
【题目】已知:抛物线y1=x2+2x-3与x轴交于A、B两点(点A在点B的左侧)，抛物线y2=x2-2ax-1(a>0)与x轴交于C、D两点(点C在点D的左侧)，在使y1>0且y2≤0的x的取值范围内恰好只有一个整数时，a的取值范围是（ ）
A. 0<a≤
B. a≥C. ≤a＜
D. <a≤
【答案】C
【解析】
根据题意可知
的对称轴为
可知使y1>0且y2≤0的x的取值范围内恰好只有一个整数时，只要符合将
代入中，使得
，且将
代入中使得
即可求出a的取值范围.
由题意可知的对称轴为
可知对称轴再y轴的右侧，
由
与x轴交于A、B两点(点A在点B的左侧)可知当
时
可求得
使
的x的取值范围内恰好只有一个整数时
只要符合将代入中，使得，且将代入中使得
即
求得解集为：
故选：C
练习册系列答案
53随堂测系列答案
相关题目
