题目内容
如图所示,菱形ABCD的边长为6厘米,∠B=60度.从初始时刻开始,点P、Q同时从A点出发,点P以1厘米/秒的速度沿A→C→B的方向运动,点Q以2厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动,设P、Q运动的时间为x秒时,△APQ与△ABC重叠部分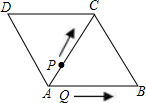 的面积为y平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:
的面积为y平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:(1)点P、Q从出发到相遇所用时间是
(2)点P、Q从开始运动到停止的过程中,当△APQ是等边三角形时x的值是
(3)求y与x之间的函数关系式.
分析:(1)菱形ABCD的边长为6厘米,∠B=60°,则易证△ABC是等边三角形,边长是6厘米.点P、Q从出发到相遇,即两人所走的路程的和是18cm.设从出发到相遇所用的时间是x秒.列方程就可以求出时间.
(2)当P在AC上,Q在AB上时,AP≠AQ,则一定不是等边三角形,当△APQ是等边三角形时,Q一定在边CD上,P一定在边CB上,若△APQ是等边三角形,则CP=DQ,根据这个相等关系,就可以得到一个关于x的方程,就可以得到x的值.
(3)求y与x之间的函数关系式.应根据0≤x<3和3≤x<6以及6≤x≤9三种情况进行讨论.把x当作已知数值,就可以求出y.就可以得到函数的解析式.
(2)当P在AC上,Q在AB上时,AP≠AQ,则一定不是等边三角形,当△APQ是等边三角形时,Q一定在边CD上,P一定在边CB上,若△APQ是等边三角形,则CP=DQ,根据这个相等关系,就可以得到一个关于x的方程,就可以得到x的值.
(3)求y与x之间的函数关系式.应根据0≤x<3和3≤x<6以及6≤x≤9三种情况进行讨论.把x当作已知数值,就可以求出y.就可以得到函数的解析式.
解答: 解:(1)∵四边形ABCD是菱形
解:(1)∵四边形ABCD是菱形
∴AB=BC
又∵∠B=60°,
∴△ABC是等边三角形,
因而边长是6.设点P,Q从出发到相遇所用的时间是x秒.
根据题意得到x+2x=18,解得x=6秒.
(2)若△APQ是等边三角形,
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP,
则CP=DQ,即x-6=18-2x,解得x=8;
(3)①当0≤x<3时,
y=S△AP1Q1=
AP1×AQ1×sin60°=
x2x
=
x2.(5分)
②当3≤x<6时,
y=S△AP2Q2
=
AP2×P2Q2
=
AP2 ×CQ2sin60°
=
x(12-2x)
=-
x2+3
x(7分)
③当6≤x≤9时,设P3Q3与AC交于点O.
(解法一)
过Q3作Q3E∥CB交AC于E,则△CQ3E为等边三角形.
∴Q3E=CE=CQ3=2x-12
∵Q3E∥CB
∴△COP3∽△EOQ3
∴
=
=
=
∴OC=
CE=
(2x-12)
y=S△AOP3
=S△ACP3-S△COP3
=
CP3×ACsin60°-
OC×CP3sin60°
=
(x-6)×6×
-
×
(2x-12)(x-6)×
=-
x2+
x-15
;
(解法二)
如图,过点O作OF⊥CP3于点F,OG⊥CQ3,于点G,
过点P3作P3H⊥DC交DC延长线于点H.
∵∠ACB=∠ACD
∴OF=OG
又CP3=x-6,CQ3=2x-12=2(x-6),
∴S△COP3=
S△COQ3
∴S△COP3=
S△CP3Q3
=
×
×CQ3×P3H
=
×
(2x-12)(x-6)×
=
(x-6)2
又S△ACP3=
CP3×AC×sin60°
=
(x-6)×6×
=
(x-6)
∴y=S△AOP3
=S△ACP3-S△OCP3
=
(x-6)-
(x-6)2
=-
x2+
x-15
(10分)
 解:(1)∵四边形ABCD是菱形
解:(1)∵四边形ABCD是菱形∴AB=BC
又∵∠B=60°,
∴△ABC是等边三角形,
因而边长是6.设点P,Q从出发到相遇所用的时间是x秒.
根据题意得到x+2x=18,解得x=6秒.
(2)若△APQ是等边三角形,
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP,
则CP=DQ,即x-6=18-2x,解得x=8;
(3)①当0≤x<3时,
y=S△AP1Q1=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
②当3≤x<6时,
y=S△AP2Q2
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=-
| ||
| 2 |
| 3 |
③当6≤x≤9时,设P3Q3与AC交于点O.
(解法一)
过Q3作Q3E∥CB交AC于E,则△CQ3E为等边三角形.
∴Q3E=CE=CQ3=2x-12
∵Q3E∥CB
∴△COP3∽△EOQ3
∴
| OC |
| OE |
| CP3 |
| EQ3 |
| x-6 |
| 2x-12 |
| 1 |
| 2 |
∴OC=
| 1 |
| 3 |
| 1 |
| 3 |
y=S△AOP3
=S△ACP3-S△COP3
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
=-
| ||
| 6 |
7
| ||
| 2 |
| 3 |
(解法二)
如图,过点O作OF⊥CP3于点F,OG⊥CQ3,于点G,
过点P3作P3H⊥DC交DC延长线于点H.
∵∠ACB=∠ACD
∴OF=OG
又CP3=x-6,CQ3=2x-12=2(x-6),
∴S△COP3=
| 1 |
| 2 |
∴S△COP3=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 6 |
又S△ACP3=
| 1 |
| 2 |

=
| 1 |
| 2 |
| ||
| 2 |
=
3
| ||
| 2 |
∴y=S△AOP3
=S△ACP3-S△OCP3
=
3
| ||
| 2 |
| ||
| 6 |
=-
| ||
| 6 |
7
| ||
| 2 |
| 3 |
点评:本题主要考查了利用图形的关系求函数的解析式.注意数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件
23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件 30、如图所示,以△ABC的三边为边,分别作三个等边三角形.
30、如图所示,以△ABC的三边为边,分别作三个等边三角形.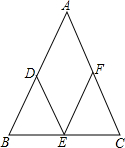 已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC边上的中点.
已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC边上的中点. 49、如图所示,在△ABC中,AB=AC,P为BC的中点,PE⊥AB于E,PF⊥AC于F,EM⊥AC于M,FN⊥AB于N,EM与FN相交于点Q,那么四边形PEQF是菱形吗?说明你的理由.
49、如图所示,在△ABC中,AB=AC,P为BC的中点,PE⊥AB于E,PF⊥AC于F,EM⊥AC于M,FN⊥AB于N,EM与FN相交于点Q,那么四边形PEQF是菱形吗?说明你的理由. 26、如图所示,Rt△ABC中,∠BAC=Rt∠,AD⊥BC于点D,∠ABC的平分线交AD于O,交AC于E,OG∥AC交BC于G.
26、如图所示,Rt△ABC中,∠BAC=Rt∠,AD⊥BC于点D,∠ABC的平分线交AD于O,交AC于E,OG∥AC交BC于G.