题目内容
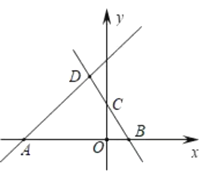
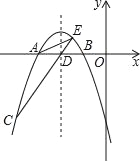
【题目】如图,抛物线y=﹣![]() x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(﹣6,0),点C的坐标是(﹣8,﹣6).
x2+bx+c交x轴于A,B两点,并经过点C,已知点A的坐标是(﹣6,0),点C的坐标是(﹣8,﹣6).
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标及点B的坐标;
(3)设抛物线的对称轴与x轴交于点D,连接CD,并延长CD交抛物线于点E,连接AC,AE,求△ACE的面积;
(4)抛物线上有一个动点M,与A,B两点构成△ABM,是否存在S△ADM=![]() S△ACD?若存在,请求出点M的坐标;若不存在,请说明理由.
S△ACD?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=﹣![]() x2﹣4x﹣6;
x2﹣4x﹣6;
(2)B(﹣2,0);
(3)S△ACE= 7.5;
(4)点M的坐标为(﹣3,![]() )或(﹣5,
)或(﹣5,![]() )或(﹣4+
)或(﹣4+![]() ,﹣
,﹣![]() )或(﹣4﹣
)或(﹣4﹣![]() ,﹣
,﹣![]() )时,S△ADM=
)时,S△ADM=![]() S△ACD.
S△ACD.
【解析】试题分析:(1)利用待定系数法进行求解即可得;
(2)化为顶点式即可得到顶点坐标,令y=0,解方程即可得;
(3)求出直线CE的解析式,然后求出与x轴的交点坐标,利用S△ACE=S△ADE+S△ACD进行计算即可得;
(4)设M(x,﹣![]() x2﹣4x﹣6),根据S△ABM=
x2﹣4x﹣6),根据S△ABM=![]() S△ACD,通过计算即可得.
S△ACD,通过计算即可得.
试题解析:(1)根据题意得![]() ,解得
,解得![]() ,
,
所以抛物线解析式为y=﹣![]() x2﹣4x﹣6;
x2﹣4x﹣6;
(2)y=﹣![]() (x+4)2+2,则抛物线的顶点坐标为(﹣4,2);
(x+4)2+2,则抛物线的顶点坐标为(﹣4,2);
当y=0时,﹣![]() x2﹣4x﹣6=0,解得x1=﹣6, x2=﹣2,则B(﹣2,0);
x2﹣4x﹣6=0,解得x1=﹣6, x2=﹣2,则B(﹣2,0);
(3)设直线CD的解析式为y=mx+n,
把D(﹣4,0),C(﹣8,﹣6)代入得![]() ,解得
,解得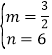 ,
,
所以直线CD的解析式为y=![]() x+6,
x+6,
解方程组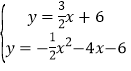 得
得![]() 或
或![]() ,则E(﹣3,
,则E(﹣3,![]() ),
),
所以S△ACE=S△ADE+S△ACD=![]() ×2×
×2×![]() +
+![]() ×2×6=7.5;
×2×6=7.5;
(4)存在.
设M(x,﹣![]() x2﹣4x﹣6),
x2﹣4x﹣6),
∵S△ABM=![]() S△ACD,
S△ACD,
∴![]() ×4|﹣
×4|﹣![]() x2﹣4x﹣6|=
x2﹣4x﹣6|=![]() ×
×![]() ×2×3,
×2×3,
当﹣![]() x2﹣4x﹣6=
x2﹣4x﹣6=![]() ,解得x1=﹣3,x2=﹣5,此时M点坐标(﹣3,
,解得x1=﹣3,x2=﹣5,此时M点坐标(﹣3,![]() )或(﹣5,
)或(﹣5,![]() );
);
当﹣![]() x2﹣4x﹣6=﹣
x2﹣4x﹣6=﹣![]() ,解得x1=﹣4+
,解得x1=﹣4+![]() ,x2=﹣4﹣
,x2=﹣4﹣![]() ,此时M点坐标(﹣4+
,此时M点坐标(﹣4+![]() ,﹣
,﹣![]() )或(﹣4﹣
)或(﹣4﹣![]() ,﹣
,﹣![]() ),
),
综上所述,点M的坐标为(﹣3,![]() )或(﹣5,
)或(﹣5,![]() )或(﹣4+
)或(﹣4+![]() ,﹣
,﹣![]() )或(﹣4﹣
)或(﹣4﹣![]() ,﹣
,﹣![]() )时,S△ADM=
)时,S△ADM=![]() S△ACD.
S△ACD.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案